题目内容
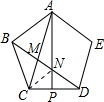
如图，ABCD为正五边形，点P为CD中点，连接BD，分别与AC、AP相交于点M、N，则
=______．
| MN |
| BM |
∵ABCD为正五边形，点P为CD中点，
∴∠BCA=∠BAC=36°，∠BAE=∠ABC=∠BCD=∠CDE=∠E=108°，
AP是CD的垂直平分线，
∴CN=ND，
∴∠NDC=∠NCD=36°，
∴∠BCN=∠BNC=72°，
∴∠CBN=36°，
∵∠NCM=108°-∠BCA-∠NCD=36°，
∠CNM=∠NCD+∠NDC=72°，
∴∠CMN=72°，
∴∠NCM=∠CBN，∠BCN=∠CNM，
∴△CNM∽△BCN，
=
，
设BC=1，CN=BM=CM=x，则MN=1-x，
∴
=
，
∴x2+x-1=0，
解得：x=
，
∴MN=1-
=
，
∴则
=
=
，
故答案为：
．
∴∠BCA=∠BAC=36°，∠BAE=∠ABC=∠BCD=∠CDE=∠E=108°，
AP是CD的垂直平分线，
∴CN=ND，
∴∠NDC=∠NCD=36°，
∴∠BCN=∠BNC=72°，
∴∠CBN=36°，
∵∠NCM=108°-∠BCA-∠NCD=36°，
∠CNM=∠NCD+∠NDC=72°，
∴∠CMN=72°，
∴∠NCM=∠CBN，∠BCN=∠CNM，
∴△CNM∽△BCN，
| MN |
| CN |
| CN |
| BN |
设BC=1，CN=BM=CM=x，则MN=1-x，
∴
| 1-x |
| x |
| x |
| 1 |
∴x2+x-1=0，
解得：x=
-1+
| ||
| 2 |
∴MN=1-
-1+
| ||
| 2 |
3-
| ||
| 2 |
∴则
| MN |
| BM |
| ||||
|
| ||
| 2 |
故答案为：
| ||
| 2 |
练习册系列答案
快乐5加2金卷系列答案
相关题目
