题目内容
（1）如图，在等腰梯形ABCD中，AD∥BC，M是AD的中点，
求证：MB=MC．
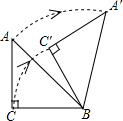
（2）如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为（4，2）．
①画出△OAB向下平移3个单位后的△O1A1B1；
②画出△OAB绕点O逆时针旋转90°后的△OA2B2，并求点A旋转到点A2所经过的路线长（结果保留π）．
求证：MB=MC．
（2）如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为（4，2）．
①画出△OAB向下平移3个单位后的△O1A1B1；
②画出△OAB绕点O逆时针旋转90°后的△OA2B2，并求点A旋转到点A2所经过的路线长（结果保留π）．
（1）证明：∵四边形ABCD是等腰梯形，
∴AB=DC，∠A=∠D．
∵M是AD的中点，
∴AM=DM．
在△ABM和△DCM中，
∴△ABM≌△DCM（SAS）．
∴MB=MC．
（2）①如下图；②图略；
点A旋转到点A2所经过的路线长=
π•4=2π．
∴AB=DC，∠A=∠D．
∵M是AD的中点，
∴AM=DM．
在△ABM和△DCM中，
|
∴MB=MC．
（2）①如下图；②图略；
点A旋转到点A2所经过的路线长=
| 90 |
| 180 |
练习册系列答案
相关题目
示意图，其中四边形AMND是矩形，弧AmD是半圆．
