题目内容
【题目】已知下面四个图形中,AB∥CD,探究四个图形中,∠APC与∠PAB,∠PCD的数量关系.
(1)图①中,∠APC与∠PAB,∠PCD的关系是__________________;
(2)图②中,∠APC与∠PAB,∠PCD的关系是__________________;
(3)请你在图③和图④中任选一个,说明∠APC与∠PAB,∠PCD的关系,并加以证明



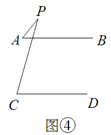
【答案】 ∠APC = ∠PAB+∠PCD; ∠APC +∠PAB+∠PCD = 360°
【解析】分析:(1)、过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,内错角相等可得∠PAB=∠APE,∠PCD=∠CPE,然后根据∠APC=∠APE+∠CPE整理即可;(2)、过点P作PE∥AB,根据平行公理可得AB∥PE∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APE=180°,∠PCD+∠CPE=180°,然根据∠APC=∠APE+∠CPE整理即可;(3)、图(3)过点P作PM∥AB,根据平行公理可得AB∥PM∥CD,再根据两直线平行,同旁内角互补∠PAB+∠APM=180°,∠PCD+∠CPM=180°,然根据∠APC=∠CPM-∠APM整理即可.
详解:(1)∠APC = ∠PAB+∠PCD; (2)∠APC +∠PAB+∠PCD = 360°;
(3)如图∠PAB =∠PCD+∠APC ,
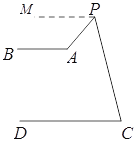
理由是:过点P作PM∥AB, ∵PM∥AB, ∴AB∥CD , ∴PM∥CD,
∴∠BAP+∠MPA= 180°,∠PCD+∠APC+∠MPA= 180°, ∴∠BAP = ∠PCD+∠APC.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目

