题目内容
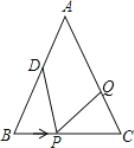
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
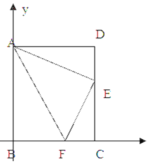
(1)求证:平行四边形ABCD是矩形;
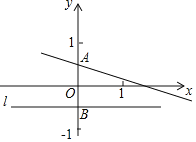
(2)如图2,以点B为坐标原点,水平方向、竖直方向为x轴、y轴建立平面直角坐标系,求直线AF的解析式;
(3)在(2)中的坐标系内是否存在这样的点P,使得以点P、A、E、F为顶点的四边形是平行四边形?若不存在,请说明理由;若存在,直接写出点P的坐标。
【答案】(1)见解析;(2) y=-2x+10 (3)见解析.
【解析】
(1)根据翻折变换的对称性可知AE=AB,在△ADE中,利用勾股定理逆定理证明三角形为直角三角形,再根据有一个角是直角的平行四边形是矩形证明即可;
(2)设BF为x,分别表示出EF、EC、FC,然后在△EFC中利用勾股定理列式进行计算,而后得出F点的坐标,利用待定系数法求解即可;
(3)分三种情况:①当以AE为对角线时;②当以AF为对角线时;③当以EF为对角线时,讨论解答即可.
(1)证明:∵把纸片ABCD折叠,使点B恰好落在CD边上,
∴AE=AB=10,AE2=102=100,
又∵AD2+DE2=82+62=100,
∴AD2+DE2=AE2,
∴△ADE是直角三角形,且∠D=90°,
又∵四边形ABCD为平行四边形,
∴平行四边形ABCD是矩形(有一个角是直角的平行四边形是矩形);
(2)解:设BF=x,则EF=BF=x,EC=CD-DE=10-6=4cm,FC=BC-BF=8-x,
在Rt△EFC中,EC2+FC2=EF2,
即42+(8-x)2=x2,
解得x=5,
故BF=5cm;
∴F(5,0),易求直线AF的解析式为:y=-2x+10;
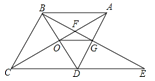
(3)如图所示:
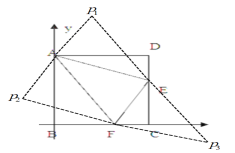
由题意得:A(0,10), E(8,4),F(5,0)
①当以AE为对角线时,
∵四边形AFE![]() 为平行四边形,∴AF=E
为平行四边形,∴AF=E![]() =
=![]() =5
=5![]() ,EF=A
,EF=A![]() =
=![]() ,∵F(5,0),E(8,4),可以看作点F的坐标向右平移3个单位,再向上平移4个单位得到,∴由A(0,10)向右平移3个单位,再向上平移4个单位得到点
,∵F(5,0),E(8,4),可以看作点F的坐标向右平移3个单位,再向上平移4个单位得到,∴由A(0,10)向右平移3个单位,再向上平移4个单位得到点![]() (0+3,10+4),即
(0+3,10+4),即![]() (3,14);
(3,14);
②当以AF为对角线时,
∵四边形AEF![]() 为平行四边形,∴AF=F
为平行四边形,∴AF=F![]() ,EF=A
,EF=A![]() ,∵A(0,10),E(8,4),可以看作点E的坐标向左平移8个单位,向上平移6个单位,得到,∴由F(5,0)向左平移8个单位,再向上平移6个单位得到点
,∵A(0,10),E(8,4),可以看作点E的坐标向左平移8个单位,向上平移6个单位,得到,∴由F(5,0)向左平移8个单位,再向上平移6个单位得到点![]() (5-8,0+6),即
(5-8,0+6),即![]() (-3,6);
(-3,6);
③当以EF为对角线时,
∵四边形AE![]() F为平行四边形,∴AF=F
F为平行四边形,∴AF=F![]() ,AF=E
,AF=E![]() ,∵A(0,10),E(8,4),可以看作点A的坐标向右平移8个单位,再向下平移6个单位得到,∴由F(5,0) 向右平移8个单位,再向下平移6个单位得到点
,∵A(0,10),E(8,4),可以看作点A的坐标向右平移8个单位,再向下平移6个单位得到,∴由F(5,0) 向右平移8个单位,再向下平移6个单位得到点![]() (5+8,0-6),即
(5+8,0-6),即![]() (13,-6);
(13,-6);
综上所述:P1(3,14),P2(-3,6),P3(13,-6)

【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
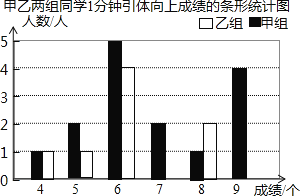
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.