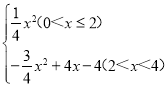题目内容
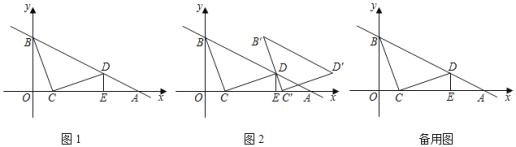
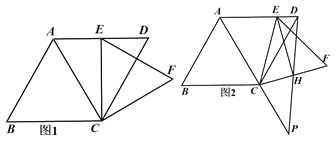
【题目】在Rt△ABC中,∠ACB=90°,AC=2,BC=4.点D是线段BC上的一个动点.点D与点B、C不重合,过点D作DE⊥BC交AB于点E,将△ABC沿着直线DE翻折,使点B落在直线BC上的F点.
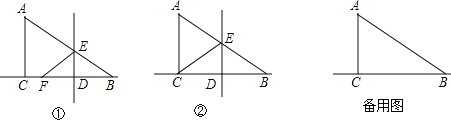
(1)设∠BAC=α(如图①),求∠AEF的大小;(用含α的代数式表示)
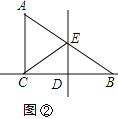
(2)当点F与点C重合时(如图②),求线段DE的长度;
(3)设BD=x,△EDF与△ABC重叠部分的面积为S,试求出S与x之间函数关系式,并写出自变量x的取值范围.
【答案】(1)1800-2α.(2)1;(3)S=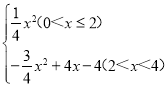
【解析】
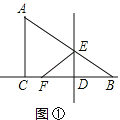
试题分析:(1)首先在Rt△ABC中,判断出∠ABC=90°-∠BAC=90°-α;然后根据翻折的性质,可得∠EFB=∠EBF;最后根据三角形外角的性质,可得∠AEF=∠EFB+∠EBF,据此解答即可.
(2)当点F与点C重合时,BD=CD时,判断出AC∥ED,即可判断出AE=BE;然后根据三角形中位线定理,求出线段DE的长度是多少即可.
(3)根据题意,分两种情况:①当点F在AC的右侧时,即0<x≤2时;②当点F在AC的左侧时,即2<x<4时;然后分类讨论,求出S与x之间函数关系式,并写出自变量x的取值范围即可.
试题解析:(1)如图①,
 ,
,
在Rt△ABC中,
∠ABC=90°-∠BAC=90°-α,
∵将△ABC沿着直线DE翻折,使点B落在直线BC上的F点,
∴∠EFB=∠EBF,
∴∠AEF=∠EFB+∠EBF=2∠EBF=2(900-∠BAC)=1800-2α.
(2)如图②,
 ,
,
当点F与点C重合时,BD=CD时,
∵ED⊥BC,AC⊥BC,
∴AC∥ED,
∴AE=BE,
∴DE=![]() AC=
AC=![]() ×2=1.
×2=1.
(3)当点F与点C重合时,
BD=CD=![]() BC=
BC=![]() ×4=2.
×4=2.
①如图③,
 ,
,
当点F在AC的右侧时,即0<x≤2时,重叠部分是△EDF.
∵AC∥ED,
∴△ABC∽△EDB,
∴![]() ,
,
即![]() ,
,
∴ED=![]() ,
,
∴S△EDF=![]() ×ED×DF=
×ED×DF=![]() ×
×![]() ×x=
×x=![]() x2,(0<x≤2).
x2,(0<x≤2).
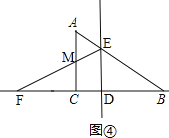
②如图④,
 ,
,
当点F在AC的左侧时,即2<x<4时,
设EF与AC相交于点M,
则重叠部分是四边形EDCM.
∴FC=FD-CD=x-(4-x)=2x-4
∵∠ACB=∠MCF=90°,∠EFB=∠EBF,
∴△ABC∽△MFC,
∴![]() ,
,
即![]() ,
,
∴MC=x-2,
∴S四边形EDCF=S△EDF-S△EDF
=![]() ×x×
×x×![]() -
-![]() ×(x-2)×(2x-4)
×(x-2)×(2x-4)
=-![]() x2+4x-4,(2<x<4).
x2+4x-4,(2<x<4).
综上,可得
S=