题目内容
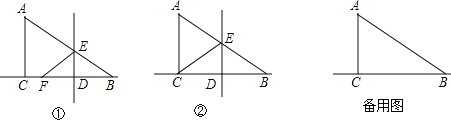
【题目】在菱形ABCD中,∠B=60,E是边CD上一点,以CE为边作等边△CEF.
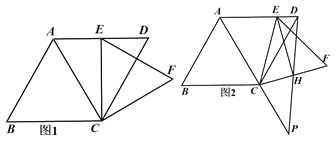
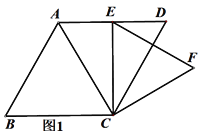
(1) 如图1,当CE⊥AD ,CF=![]() 时,求菱形ABCD的面积;
时,求菱形ABCD的面积;
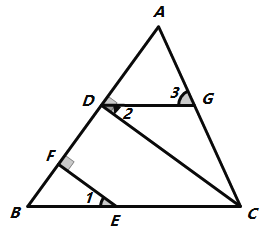
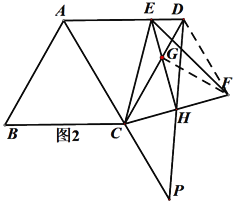
(2) 如图2,过点E作∠CEF的平分线交CF于H,连接DH,并延长DH与AC的延长交于点P,若∠ECD=15,求证:![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由等边三角形的性质得出CE的长.再由菱形的性质及∠B=60得到CD的长,根据菱形的面积公式即可得出结论.
(2)连接DF,过F作FG⊥CD于G.由菱形的性质及∠B=60得到△ABC和△ACD是等边三角形,即可证明△ACE≌△DCF,进而得到DF//AP,由平行线的性质得到∠FDH=∠CPH.
由等边三角形的性质得到CH=HF.可证明△CHP≌△FHD,得到DF=CP.在Rt△DGF中,由∠FDC=60,可得![]() .在等腰Rt△CFG中,有
.在等腰Rt△CFG中,有![]() ,从而可以得出结论.
,从而可以得出结论.
(1)∵等边△CEF,CF=![]() ,∴CE=CF=
,∴CE=CF=![]() .
.
∵菱形ABCD,∠B=60,∴∠D=∠B=60,AD=CD.
∵CE⊥AD,∴∠ECD=30,∴CD=4,∴AD=4,∴S菱形ABCD=ADCE=![]() .
.
(2)连接DF,过F作FG⊥CD于G.
∵菱形ABCD,∴AB=BC=CD=AD.
∵∠B=60,∴△ABC和△ACD是等边三角形,∴∠CAD=∠ACD=60.
∵等边△CEF,∴CE=CF,∠ECF=60,∴∠ACD-∠ECD=∠ECF-∠ECD即∠ACE=∠DCF.
在△ACE与△DCF中,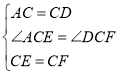 ,∴△ACE≌△DCF,∴∠FDC=60.
,∴△ACE≌△DCF,∴∠FDC=60.
∵∠ACD=60,∴DF//AP,∴∠FDH=∠CPH.
∵等边△CEF,EH平分∠CEF,∴CH=HF.
在△CHP与△FHD中,∵∠FDH=∠CPH,∠FHD=∠CHP,HF=CH,∴△CHP≌△FHD,∴DF=CP.
∵∠FDC=60,FG⊥CD,∴![]() .
.
∵∠ECF=60,∠ECD=15,∴∠DCF=45.
∵∠DCF=45,FG⊥CD,∴![]() ,∴
,∴![]() .
.

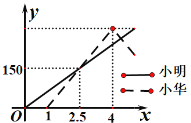
【题目】为缓解油价上涨给出租车行业带来的成本压力,某市拟调整出租车运价,调整方案见下列表格及图象(其中![]() 为常数)
为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过 | 起步价7元 | 起步价 |
超过 | 每公里2元 | 每公里 |
超出 | 每公里 | |
设行驶路程为![]() ,调价前的运价
,调价前的运价![]() (元),调价后运价
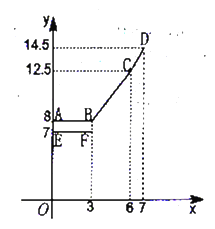
(元),调价后运价![]() (元),如图,折线
(元),如图,折线![]() 表示
表示![]() 与
与![]() 之间的函数关系式,线段
之间的函数关系式,线段![]() 表示当
表示当![]() 时,
时,![]() 与
与![]() 的函数关系式,根据图表信息,完成下列各题:
的函数关系式,根据图表信息,完成下列各题:
①填空:![]() ,
,![]() ,
,![]() ;
;
②当![]() 时,求
时,求![]() 与
与![]() 的关系,补充图中该函数的图像;
的关系,补充图中该函数的图像;
③函数![]() 与
与![]() 的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.
的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义;若不存在,请说明理由.