题目内容
 推理填空:
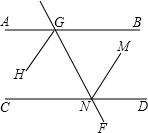
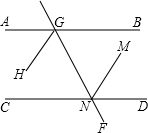
推理填空:如图,AB∥CD,EF分别交AB、CD于G、N,GH、NM分别平分∠AGN,∠GND.
求证:GH∥NM.
证明:∵AB∥CD(
∴∠AGN=∠GND(
∵GH,NM分别平分∠AGN,∠GND
∴∠HGN=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠HGN=∠MNG
∴GH∥NM(
分析:首先根据已知,得内错角相等,再结合角平分线定义,得到∠HGN=∠MNG,从而根据内错角相等,得两条直线平行.
解答:证明:∵AB∥CD( 已知),
∴∠AGN=∠GND( 两直线平行,内错角相等);
∵GH,NM分别平分∠AGN,∠GND,
∴∠HGN=
∠AGN,∠MNG=
∠GND( 角平分线定义),
∴∠HGN=∠MNG,
∴GH∥NM( 内错角相等,两直线平行).
∴∠AGN=∠GND( 两直线平行,内错角相等);
∵GH,NM分别平分∠AGN,∠GND,
∴∠HGN=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠HGN=∠MNG,
∴GH∥NM( 内错角相等,两直线平行).
点评:此题综合运用了平行线的性质和判定.

练习册系列答案
相关题目
 19、推理填空:
19、推理填空: 23、推理填空.如图,已知AB⊥BC,CD⊥BC,∠1=∠2,求证:EB∥FC.
23、推理填空.如图,已知AB⊥BC,CD⊥BC,∠1=∠2,求证:EB∥FC.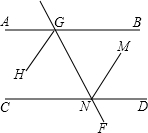 推理填空:
推理填空: ∠AGN,∠MNG=
∠AGN,∠MNG=