题目内容
【题目】知识准备:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() .则
.则![]() 两点之间的距离表示为:
两点之间的距离表示为:![]()
问题探究:数轴上![]() 两点对应的数分别为
两点对应的数分别为![]() 且
且![]() 满足
满足![]()
![]() 直接写出:
直接写出:![]() ___、
___、![]()
![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,请问:当点
,请问:当点![]() 到
到![]() 两点的距离和为
两点的距离和为![]() 时,
时,![]() 满足什么条件?请利用数轴进行说明(此时
满足什么条件?请利用数轴进行说明(此时![]() 最小).
最小).
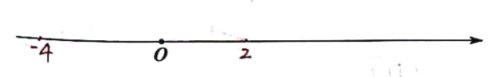
拓展:当数轴上 应用:国庆期间汉口江滩武汉关至长江二桥之间是观看“70周年国庆灯光秀”的理想区域,武汉关与长江二桥相距约 【答案】问题探究:(1) 【解析】 问题探究: 问题探究: 点P到A、B两点的距离和为6时,点P在AB之间(包括A,B两点),即![]() 三点对应的数分别为
三点对应的数分别为![]() 在数轴上有一点
在数轴上有一点![]() 对应的数为
对应的数为![]() ,当
,当![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?
的值最小? 
![]() 公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔
公里。在国庆期间,为了服务广大市民,汉口江滩管理处在汉口江滩武汉关至长江二桥之间每隔![]() 公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作
公里安排了便民服务小组(武汉关与长江二桥不安排) ,还需要设置一个便民服务物资站,请问便民服务物资站应该设置在什么地方,使它到各个便民服务小组的距离和最小,最小值是多少公里?便民服务物资站位置代表的数记作![]() 利用下图直接给出结果:
利用下图直接给出结果:![]() 满足的条件: 最小值为 公里.
满足的条件: 最小值为 公里.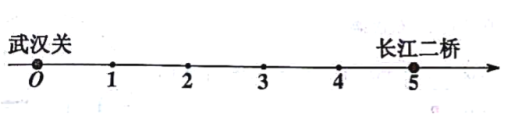
![]() ,
,![]() ; (2)
; (2)![]() ;拓展:当
;拓展:当![]() 时,
时,![]() 最小时为
最小时为![]() ;应用:
;应用:![]() ;4
;4
(1)根据非负数的性质可得![]() 和
和![]() 的值;
的值;
(2)根据绝对值的几何意义,可得当点P在AB之间(包括A,B两点),P到A点与P到B点的距离之和是6,即PA+PB最小;
拓展:点P在点A和点B(含点A和点B)之间,依此即可求解.
应用:同理根据拓展的问题,分情况即可求解.
(1)∵![]() .
.
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)如图1,
![]() ,此时PA+PB最小;
,此时PA+PB最小;
拓展:
点P表示的数为2,该最小值为12,
设P到A、B、C的距离和为d,
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
③当![]() 时,
时,![]() >12,
>12,
④当x>8时![]() >18;
>18;
综上,当点P表示的数为2时,P到A、B、C的距离和最小,最小值为12.
应用:
如图3,设便民服务物资站为点P,各便民服务小组分别为A,B,C,D,
设P到A、B、C、D的距离和为d,
则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
②当![]() 时,
时,![]() >4,
>4,
③当![]() 时,
时,![]() ,
,
④当![]() 时,
时,![]() >4,
>4,
⑤当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ;
;
综上,![]() 满足的条件:
满足的条件:![]() ,最小值为4公里.
,最小值为4公里.
故答案为:![]() ,4.
,4.

西城学科专项测试系列答案
小考必做系列答案
小考实战系列答案
小考复习精要系列答案
小考总动员系列答案
小升初必备冲刺48天系列答案
68所名校图书小升初高分夺冠真卷系列答案
伴你成长周周练月月测系列答案
小升初金卷导练系列答案
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
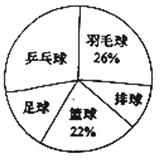
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.