题目内容
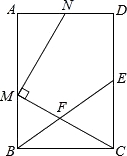
【题目】如图(1)AB=9cm,AC⊥AB,BD⊥AB,AC=BD=7cm,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,它们运动的时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由;
(2)在(1)的前提条件下,判断此时线段PC和线段PQ的位置关系,并证明;
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=50°”,其他条件不变.设点Q的运动速度为xcm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
【答案】(1)△ACP与△BPQ全等,理由见解析;(2)PC⊥PQ,证明见解析;(3)存在,当t=1s,x=2cm/s或t=![]() s,x=
s,x=![]() cm/s时,△ACP与△BPQ全等.
cm/s时,△ACP与△BPQ全等.
【解析】
(1)利用![]() 定理证明
定理证明![]() ;
;
(2)根据全等三角形的性质判断线段![]() 和线段
和线段![]() 的位置关系;
的位置关系;
(3)分![]() ,
,![]() 两种情况,根据全等三角形的性质列式计算.
两种情况,根据全等三角形的性质列式计算.
(1)△ACP与△BPQ全等,
理由如下:当t=1时,AP=BQ=2,
则BP=9﹣2=7,
∴BP=AC,
又∵∠A=∠B=90°,
在△ACP和△BPQ中,
 ,
,
∴△ACP≌△BPQ(SAS);
(2)PC⊥PQ,
证明:∵△ACP≌△BPQ,
∴∠ACP=∠BPQ,
∴∠APC+∠BPQ=∠APC+∠ACP=90°.
∴∠CPQ=90°,
即线段PC与线段PQ垂直;
(3)①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
∴9﹣2t=7,
解得,t=1(s),则x=2(cm/s);
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
则2t=![]() ×9,
×9,
解得,t=![]() (s),则x=7÷
(s),则x=7÷![]() =
=![]() (cm/s),
(cm/s),
故当t=1s,x=2cm/s或t=![]() s,x=
s,x=![]() cm/s时,△ACP与△BPQ全等.
cm/s时,△ACP与△BPQ全等.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案