��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���A����Ϊ����4��4������B������Ϊ��4��0����
��1����ֱ��AB�Ľ���ʽ��
��2����M���������ϵ�һ���㣬��ABΪֱ�DZ߹���ֱ�������Ρ�ABM��������������������е�M�����ꣻ
��3����ͼ2���Ե�AΪֱ�Ƕ�������CAD=90�㣬����AC��x��ĸ��������C������AD��y��ĸ��������D������CAD�Ƶ�A��תʱ��OC��OD��ֵ�Ƿ����仯�������䣬ֱ��д������ֵ�����仯��ֱ��д�����ı仯��Χ����Ҫ������̣���
���𰸡�
��1��
��ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0����
�ߵ�A����4��4������B��0��2����ֱ��AB�ϣ�
�� ![]() �����
����� 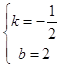 ��
��
��ֱ��AB�Ľ���ʽΪ��y=�� ![]() x+2
x+2
��2��
�ߡ�ABM����ABΪֱ�DZߵ�ֱ�������Σ�
���С�BAM=90����ABM=90�㣬
�ٵ���BAM=90��ʱ����ͼ1��
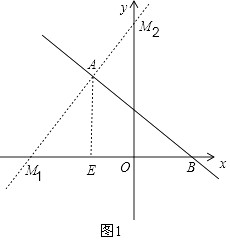
��A��AB�Ĵ��ߣ���x���ڵ�M1����y���ڵ�M2��
���֪��AEM1�ס�BEA��
�� ![]() =
= ![]() ��
��
�ɣ�1����֪OE=OB=AE=4��
�� ![]() =
= ![]() �����M1E=2��
�����M1E=2��
��OM1=2+4=6��
��M1����6��0����
��AE��y�ᣬ
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����OM2=12��
�����OM2=12��
��M2��0��12����
�ڵ���ABM=90��ʱ����ͼ2��
��B��AB�Ĵ��ߣ���y���ڵ�M3��
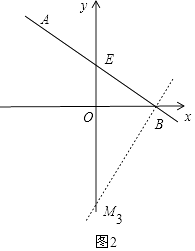
��ֱ��AB��y���ڵ�E�����ɣ�1����֪E��0��2����
��OE=2��OB=4��
�������֪��BOE�ס�M3OB��
�� ![]() =
= ![]() ����
���� ![]() =
= ![]() �����OM3=8��
�����OM3=8��
��M3��0����8����
���Ͽ�֪��M������Ϊ����6��0����0��12����0����8��
��3��
���䣮
�������£�
����A�ֱ���x�ᡢy��Ĵ��ߣ�����ֱ�ΪG��H����ͼ3��
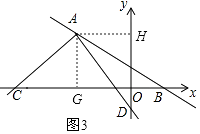
���AGC=��AHD=90�㣬
�֡ߡ�HOC=90�㣬
���GAH=90�㣬
���DAG+��DAH=90�㣬
�ߡ�CAD=90�㣬
���DAG+��CAG=90�㣬
���CAG=��DAH��
��A����4��4����
��OG=AH=AG=OH=4��
�ڡ�AGC�͡�AHD��
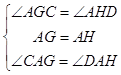
���AGC�ա�AHD��ASA����
��GC=HD��
��OC��OD=��OG+GC������HD��OH��=OG+OH=8��
��OC��OD��ֵ�������仯��ֵΪ8
����������1����A��B������������ô���ϵ���������ֱ��AB�Ľ���ʽ����2���ֱ��A��B������AB�Ĵ��ߣ���������Ľ��㼴Ϊ�����M�㣬�ٽ�����������ε��������OM�ij�������õ�M�����ꣻ��3����A�ֱ���x���y��Ĵ��ߣ�����ֱ�ΪE��F����֤����AEC�ա�AFD���ɵõ�EC=FD���Ӷ��ɰ�OC��ODת��ΪFD��OD���������߶εĺͲ�����OC��OD=OE+OF=8��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�