题目内容
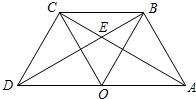 22、如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.
22、如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.分析:由于△BOC和△ABO都是等边三角形,可得OD=OC=OB=OA,进而求出∠BDA与∠CAD的大小及关系,则可求解∠AEB.
解答:解:∵△DOC和△ABO都是等边三角形,
且点O是线段AD的中点,
∴OD=OC=OB=OA,
∴△ACD≌△DBA,
∴∠BDA=∠CAD.
又∵∠BDA+∠OBD=∠BOA=60°,
而∠ODB=∠OBD,
∴∠BDA=30°.
∴∠CAD=30°.
∵∠AEB=∠BDA+∠CAD,
∴∠AEB=60°.
且点O是线段AD的中点,
∴OD=OC=OB=OA,

∴△ACD≌△DBA,
∴∠BDA=∠CAD.
又∵∠BDA+∠OBD=∠BOA=60°,
而∠ODB=∠OBD,
∴∠BDA=30°.
∴∠CAD=30°.
∵∠AEB=∠BDA+∠CAD,
∴∠AEB=60°.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,求得角的度数是正确解答本题的关键.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 如图,点B是线段AD的中点,AC、ED交于点F,∠1=∠2,EB=BC,连接FB,求证:FB⊥AD.
如图,点B是线段AD的中点,AC、ED交于点F,∠1=∠2,EB=BC,连接FB,求证:FB⊥AD.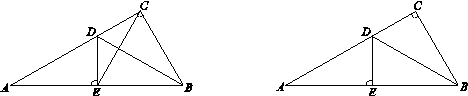
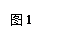
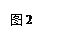
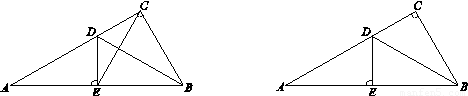
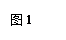
 如图,点B是线段AD的中点,AC、ED交于点F,∠1=∠2,EB=BC,连接FB,求证:FB⊥AD.
如图,点B是线段AD的中点,AC、ED交于点F,∠1=∠2,EB=BC,连接FB,求证:FB⊥AD.