��Ŀ����
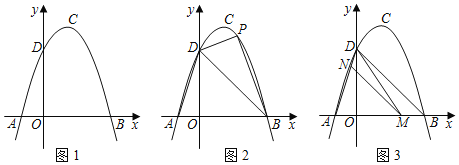
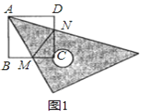
����Ŀ����1����������ABCD�У�G��CD���ϵ�һ�����㣨����C��D�غϣ�����CGΪ����������ABCD����һ��������CEFG������BG��DE����ͼ����ֱ��д���߶�BG��DE�Ĺ�ϵ ��
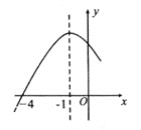
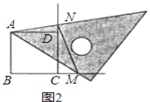
��2����ͼ���е�������CEFG�Ƶ�C��˳ʱ�뷽����ת����Ƕ�![]() ����ͼ�������жϣ�1���еĽ����Ƿ��������������ֱ��д�����ۣ�����������˵�����ɣ�
����ͼ�������жϣ�1���еĽ����Ƿ��������������ֱ��д�����ۣ�����������˵�����ɣ�
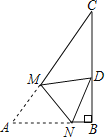
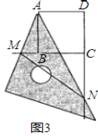
��3������1���е������ζ���Ϊ���Σ���ͼ�����ٽ�����CEFG�Ƶ�C��˳ʱ�뷽����ת����Ƕ�![]() ����ͼ������AB=a��BC=b��CE =ka��CG=kb��(
����ͼ������AB=a��BC=b��CE =ka��CG=kb��(![]() )���жϣ�1���еĽ����Ƿ���Ȼ��������˵�����ɣ�
)���жϣ�1���еĽ����Ƿ���Ȼ��������˵�����ɣ�

���𰸡���1��BG=DE�� BG��DE��(2)BG=DE�� BG��DE��(3)BG��DE������BG=DE�����������ɼ�������
��������
��1���������ε����ʵó�BC��CD��CE��CG����BCD����ECG��90�㣬��SAS֤����BCG�ա�DCE���ó�BG��DE����CBG����CDE���ӳ�BG��DE��H���ɽǵĻ����ϵ�ͶԶ������֤����CDE����DGH��90�㣬���������ڽǺͶ����ó���DHG��90�㼴�ɣ�
��2���������ε����ʿɵ�BC��CD��CE��CG����BCD����ECG��90�㣬Ȼ�������BCG����DCE����SAS֤����BCG�͡�DCEȫ�ȣ���ȫ�������ζ�Ӧ����ȿɵ�BG��DE��ȫ�������ζ�Ӧ����ȿɵá�CBG����CDE��Ȼ�������DOH��90�㣬�ٸ��ݴ�ֱ�Ķ���֤�����ɣ�
��3�����ݾ��ε�����֤����BCG�ס�DCE���õ�![]() ���������������ζ�Ӧ����ȿɵ���CBG=��CDE��Ȼ�������DOH��90�����ٸ��ݴ�ֱ�Ķ���֤�����ɣ�
���������������ζ�Ӧ����ȿɵ���CBG=��CDE��Ȼ�������DOH��90�����ٸ��ݴ�ֱ�Ķ���֤�����ɣ�
��1���⣺BG��DE��BG��DE���������£�
���ı���ABCD�������Σ��ı���CEFG�������Σ�
��BC��CD��CE��CG����BCD����ECG��90�㣬
�ڡ�BCG�͡�DCE�У�
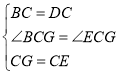 ��
��
���BCG�ա�DCE��SAS����
��BG��DE����CBG����CDE��
�ӳ�BG��DE��H����ͼ��ʾ��
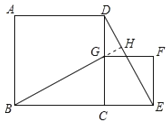
�ߡ�CBG����BGC��90�㣬��DGH����BGC��
���CDE����DGH��90�㣬
���DHG��90�㣬
��BG��DE��
��2���⣺�������������£�
���ı���ABCD�������Σ��ı���CEFG�������Σ�
��BC��CD��CE��CG����BCD����ECG��90�㣬
���BCD����DCG����ECG����DCG��
����BCG����DCE��
�ڡ�BCG�͡�DCE�У�
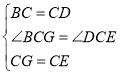 ��
��
���BCG�ա�DCE��SAS����
��BG��DE����CBG����CDE��
�ߡ�CBG����BHC��90�㣬��BHC����DHO��
���CDE����DHO��90�㣬
�ڡ�DHO�У���DOH��180������CDE����DHO����180��90�㣽90����
��BG��DE����
(3)BG��DE������BG=DE����������
���ͼ��˵�����£�
���ı���ABCD���ı���CEFG���Ǿ��Σ���AB=a��BC=b��CG=kb��CE=ka(a��b��k��0)��
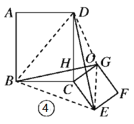
![]() ��
��
��BCD=��ECG=90����
���BCG=��DCE��
���BCG�ס�DCE����
��![]() ����CBG=��CDE��
����CBG=��CDE��
���ߡ�BHC=��DHO����CBG+��BHC=90����
���CDE+��DHO=90����
���DOH=90����
��BG��DE��