题目内容
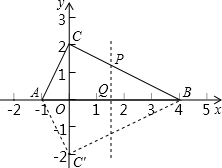
抛物线y=ax2+bx+c经过直角△ABC的顶点A（-1，0），B（4，0），直角顶点C在y轴上，若抛物线的顶点在△ABC的内部（不包括边界），则a的范围是______．
∵点A（-1，0），B（4，0），
∴OA=1，OB=4，
易得△ACO∽△CBO，
∴
=
，
即
=
，
解得OC=2，
∵抛物线y=ax2+bx+c经过A（-1，0），B（4，0），
∴对称轴为直线x=
=
，
设对称轴与直线BC相交于P，与x轴交于Q，
则BQ=4-
=2.5，
tan∠ABC=
=
，
即
=
，
解得PQ=
，
设抛物线的解析式为y=a（x+1）（x-4），
则y=a（x2-3x-4）=a（x-
）2-
a，
当点C在y轴正半轴时，0＜-
a＜
，
解得-
＜a＜0，
当点C在y轴负半轴时，-
＜-
a＜0，
解得0＜a＜
，
所以，a的取值范围是-
＜a＜0或0＜a＜
．
故答案为：-
＜a＜0或0＜a＜
．
∴OA=1，OB=4，
易得△ACO∽△CBO，
∴
| OA |
| OC |
| OC |
| OB |
即
| 1 |
| OC |
| OC |
| 4 |
解得OC=2，
∵抛物线y=ax2+bx+c经过A（-1，0），B（4，0），
∴对称轴为直线x=
| -1+4 |
| 2 |
| 3 |
| 2 |
设对称轴与直线BC相交于P，与x轴交于Q，
则BQ=4-
| 3 |
| 2 |
tan∠ABC=
| OC |
| OB |
| PQ |
| BQ |
即
| 2 |
| 4 |
| PQ |
| 2.5 |
解得PQ=
| 5 |
| 4 |
设抛物线的解析式为y=a（x+1）（x-4），
则y=a（x2-3x-4）=a（x-
| 3 |
| 2 |
| 25 |
| 4 |
当点C在y轴正半轴时，0＜-
| 25 |
| 4 |
| 5 |
| 4 |
解得-
| 1 |
| 5 |
当点C在y轴负半轴时，-
| 5 |
| 4 |
| 25 |
| 4 |
解得0＜a＜
| 1 |
| 5 |
所以，a的取值范围是-
| 1 |
| 5 |
| 1 |
| 5 |
故答案为：-
| 1 |
| 5 |
| 1 |
| 5 |
练习册系列答案
巧学巧练系列答案
相关题目
