Question

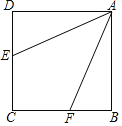
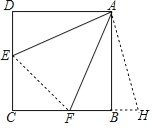
【题目】如图，已知正方形ABCD，点E，F分别在CD，BC上，且∠EAF＝∠DAE+∠BAF，则的值为（　　）

A. B. C. D.

Answer 1

【答案】A

【解析】

将△ADE旋转至△ABH，根据旋转的性质可得∠DAE＝∠BAH，AE＝AH，DE＝BH，再利用”SAS“证明△AEF≌△AHF，从而得EF＝FH，再根据勾股定理即可求CE2+CF2＝EF2，即有（CE﹣CF）2+2CECF＝（BF﹣DE）2+4BFDE，而BF﹣DE＝CE﹣CF，即可求解.

如图，连接EF，将△ADE旋转至△ABH

∴∠DAE＝∠BAH，AE＝AH，DE＝BH

∴∠EAF＝∠DAE+∠BAF＝∠BAH+∠BAF＝∠FAH

∵∠D＝∠ABC＝∠ABH＝90°

∴∠ABC+∠ABH＝180°

∴C，B，H三点共线

∵AF＝AF

∴△AEF≌△AHF（SAS）

∴EF＝FH＝FB+BH＝FB+DE

∵DE+CE＝CF+BF

∴BF﹣DE＝CE﹣CF

∵CE2+CF2＝EF2

∴CE2+CF2＝（BF+DE）2

∴（CE﹣CF）2+2CECF＝（BF﹣DE）2+4BFDE

∵BF﹣DE＝CE﹣CF

∴2CECF＝4BFDE

∴

故选：A．