题目内容
如图所示,在直角坐标系中,正方形ABOD的边长为a,O为原点,点B在x轴的负半轴上,点D在y轴的正半轴上,直线OM的解析式为y=2x,直线CN过x轴上的一点C(-| 3 |
| 5 |
| a |
| 10 |
(1)求点A、B、D的坐标;
(2)求梯形ECOD的面积;
(3)0≤t<4时,写出S与t的函数关系式.

分析:(1)根据正方形的性质得到AB=AD=BO=OD=a,即可求出答案;
(2)设直线CE的解析式是y=2x+b,把C的坐标代入得到方程0=-
a+b,求出解析式y=2x+
a,求出y=a时x的值,即可求出DE,根据梯形ECOD的面积=
(DE+OC)•OD即可求出答案;
(3)求出BC=a-
a=
a,
a÷
a=4,根据题意求出GE、CQ根据GH∥QZ,得到
=
,代入求出IZ=
t,根据s=S正方形ABOD-S梯形CQGE-S△OZI,求出即可.
(2)设直线CE的解析式是y=2x+b,把C的坐标代入得到方程0=-
| 6 |
| 5 |
| 6 |
| 5 |
| 1 |
| 2 |
(3)求出BC=a-
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 10 |
| HR |
| OZ |
| HI |
| IZ |
| a |
| 5 |
解答:(1)解:∵正方形ABOD的边长为a,
∴AB=AD=BO=OD=a,
∴A的坐标是(-a,a),B的坐标是(-a,0),D的坐标是(0,a),
答:点A、B、D的坐标分别是(-a,a),(-a,0),(0,a).
(2)解:设直线CE的解析式是y=2x+b,
把C的坐标代入得:0=-
a+b,
解得:b=
a,
∴y=2x+
a,
把y=a代入得:x=-
a,
∴DE=
a,
∴梯形ECOD的面积是
(DE+OC)•OD=
×(
a+
a)×a=
a2,
答:梯形ECOD的面积是
a2;
(3)解:BC=a-
a=
a,
a÷
a=4,
根据题意得:GE=a-
t-
a=
a-
t,
CQ=a-
a-
t=
a-
t,
∵GH∥QZ,
∴
=
,
∴
=
,
∴IZ=
t,
∴s=S正方形ABOD-S梯形CQGE-S△OZI,
=a2-
(
a-
t+
a-
t)a-
•
t•
t,
=-
t2+
t+
a2,
答:0≤t<4时,t的函数关系式是S=-
t2+
t+
a2.
∴AB=AD=BO=OD=a,
∴A的坐标是(-a,a),B的坐标是(-a,0),D的坐标是(0,a),
答:点A、B、D的坐标分别是(-a,a),(-a,0),(0,a).
(2)解:设直线CE的解析式是y=2x+b,
把C的坐标代入得:0=-
| 6 |
| 5 |
解得:b=
| 6 |
| 5 |
∴y=2x+
| 6 |
| 5 |
把y=a代入得:x=-
| 1 |
| 10 |
∴DE=
| 1 |
| 10 |
∴梯形ECOD的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 10 |
| 3 |
| 5 |
| 7 |
| 20 |
答:梯形ECOD的面积是
| 7 |
| 20 |
(3)解:BC=a-
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 10 |

根据题意得:GE=a-
| a |
| 10 |
| 1 |
| 10 |
| 9 |
| 10 |
| a |
| 10 |
CQ=a-
| 3 |
| 5 |
| a |
| 10 |
| 2 |
| 5 |
| a |
| 10 |
∵GH∥QZ,
∴
| HR |
| OZ |
| HI |
| IZ |
∴
| ||||
|
| a-IZ |
| IZ |
∴IZ=
| a |
| 5 |
∴s=S正方形ABOD-S梯形CQGE-S△OZI,
=a2-
| 1 |
| 2 |
| 2 |
| 5 |
| a |
| 10 |
| 9 |
| 10 |
| a |
| 10 |
| 1 |
| 2 |
| a |
| 10 |
| a |
| 5 |
=-
| a2 |
| 100 |
| a2 |
| 10 |
| 7 |
| 20 |
答:0≤t<4时,t的函数关系式是S=-
| a2 |
| 100 |
| a2 |
| 10 |
| 7 |
| 20 |
点评:本题主要考查对正方形的性质,用待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,三角形的面积,平行线分线段成比例定理,解一元一次方程等知识点的理解和掌握,能熟练地运用这些性质进行计算是解此题的关键,此题是一个综合性比较强的题目,题型较好.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
 sin∠BOA=
sin∠BOA= 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.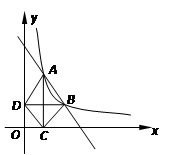

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.