Question

如图所示，在直角坐标平面内，函数的图象经过A(1，4)，B(a，b)，其中a>1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连结AD、DC、CB．

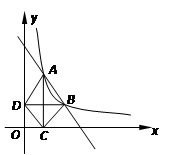
1.若△ABD的面积为4，求点B的坐标

2.求证：DC∥AB

3.四边形ABCD能否为菱形？如果能，请求出四边形ABCD 为菱形时，直线AB的函数解析式；如果不能，请说明理由．

 

Answer 1

 

1.(3，)

2.见解析

3.

解析:（1）解：∵函数y=mx(x＞0，m是常数）图象经过A（1，4），∴m=4．

设BD，AC交于点E，据题意，可得B点的坐标为(a，)，D点的坐标为(0，)，E点的坐标为(1，)，∵a＞1，

∴DB=a，AE=4-．

由△ABD的面积为4，即a(4-)=4，

得a=3，

∴点B的坐标为(3，)；

（2）AB直线的斜率=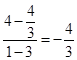，DC直线的斜率=，∴DC∥AB。

（3）四边形ABCD为菱形，对角线互相垂直平分，那么B点的坐标为（2，2）.

设直线AB的函数解析式为，把A、B两点的坐标代入得k=-2,b=6

直线AB的函数解析式.