题目内容
【题目】已知:如图,在 ![]() 中,
中, ![]() 是
是 ![]() 的中点,点
的中点,点 ![]() 在
在 ![]() 上,点
上,点 ![]() 在
在 ![]() 上,且
上,且 ![]() .
.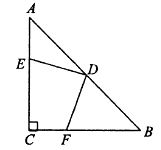
(1)求证: ![]() .
.
(2)若 ![]() =2,求四边形
=2,求四边形 ![]() 的面积.
的面积.
【答案】
(1)证明:如图,连接CD. 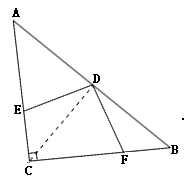 因为
因为 ![]() ,
, ![]()
所以 ![]() 是等腰直角三角形
是等腰直角三角形
所以 ![]()
因为 ![]() 为
为 ![]() 的中点
的中点
所以 ![]() ,
, ![]() 平分
平分 ![]() ,
, ![]()
所以 ![]()
又因为 ![]()
所以 ![]()
所以 ![]() ,
, ![]()
因为 ![]()
所以 ![]()
即 ![]()
(2)解:因为 ![]()
所以 ![]()
所以 ![]()
因为 ![]() 是
是 ![]() 的中点
的中点
所以 ![]()
所以 ![]()
【解析】(1)抓住已知条件等腰直角三角形ACB,D 是 AB 的中点,根据等腰三角形三线合一的性质,因此添加辅助线连接CD,易证明BD=CD=AD , CD 平分 ∠BCA , CD⊥AB,再证明 ΔADEΔCDF,得出DE=DF , ∠ADE=∠CD,然后证明∠EDF=90°,即可证得结论。
(2)根据ΔADEΔCDF,得出SΔADE=SΔCFD , 继而得出S四边形CEDF=SΔADC , 而△ACD的面积等于△ABC的面积的一半,即可得出结果。

练习册系列答案
相关题目