题目内容
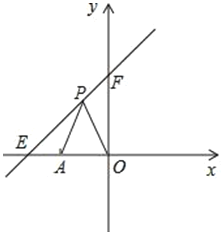
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点.
上的一个动点.

(1)求![]() 的值;
的值;
(2)点![]() 在第二象限内的直线
在第二象限内的直线![]() 上的运动过程中,写出
上的运动过程中,写出![]() 的面积
的面积![]() 与
与![]() 的函整表达式,并写出自变量
的函整表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究,当点![]() 在直线
在直线![]() 上运动到时,
上运动到时,![]() 的面积可能是
的面积可能是![]() 吗,若能,请求出点
吗,若能,请求出点![]() 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
【答案】(1)![]() ;(2)S=
;(2)S=![]() ;(3)能面积是
;(3)能面积是![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】
(1)利用待定系数法求解;(2)设P(x,y),根据一次函数解析式和三角形面积公式求出函数表达式及x的取值范围;(3)分类讨论,将S=15代入解析式,求x.
(1)点![]() 的坐标为
的坐标为![]() ,且在直线
,且在直线![]() 上,
上,
![]() ,
,
解得,![]() ;
;
(2)点![]() 是第二象限内的直线上的一个动点,
是第二象限内的直线上的一个动点,
![]() ,
,
![]() ;
;
(3) 当点![]() 在
在![]() 轴的上方时,由题意得,
轴的上方时,由题意得,![]() ,
,
解得,![]() ,
,
则![]()
当点![]() 在
在![]() 轴的下方时,
轴的下方时,![]() ,代入
,代入![]() 中,此时
中,此时![]()
![]() 的面积是
的面积是![]() 时,点
时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目




