题目内容
【题目】已知直线y=2x﹣5与x轴和y轴分别交于点A和点B，抛物线y=﹣x2+bx+c的顶点M在直线AB上，且抛物线与直线AB的另一个交点为N．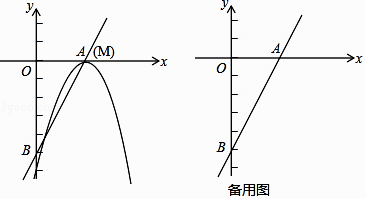
（1）如图，当点M与点A重合时，求抛物线的解析式；
（2）在（1）的条件下，求点N的坐标和线段MN的长；
（3）抛物线y=﹣x2+bx+c在直线AB上平移，是否存在点M，使得△OMN与△AOB相似？若存在，直接写出点M的坐标；若不存在，请说明理由．
【答案】
（1）
解：∵直线y=2x﹣5与x轴和y轴分别交于点A和点B，
∴A（ 
，0），B（0，﹣5）．
当点M与点A重合时，∴M（ ，0），
∴抛物线的解析式为y=﹣（x﹣ ）2，即y=﹣x2+5x﹣ 
（2）
解：N在直线y=2x﹣5上，设N（a，2a﹣5），又N在抛物线上，
∴2a﹣5=﹣a2+5a﹣ ，解得a1= 
，a2= （舍去），
∴N（ ，﹣4）．
过点N作NC⊥x轴，垂足为C，如图1
，
∵N（ ，﹣4），
∴C（ ，0），
∴NC=4．MC=OM﹣OC= ﹣ =2，
∴MN= 
= 
=2 
（3）
解：设M（m，2m﹣5），N（n，2n﹣5）．
∵A（ ，0），B（0﹣，5），
∴OA= ，OB=5，则OB=2OA，AB= 
= 
，
如图2
，
当∠MON=90°时，∵AB≠MN，且MN和AB边上的高相等，因此△OMN与△AOB不能全等，
∴△OMN与△AOB不相似，不满足题意；
当∠OMN=90°时， 
= 
，即 = 
，解得OM= ，
则m2+（2m﹣5）2=（ ）2，解得m=2，∴M（2，﹣1）；
当∠ONM=90°时， = ，即 = 
，解得ON= ，则n2+（2n﹣5）2=（ ）2，解得n=2，
∵OM2=ON2+MN2，即m2+（2m﹣5）2=5+（2 ）2，解得m=4，则M点的坐标为（4，3），
综上所述：M点的坐标为（2，﹣1）或（4，3）
【解析】（1）根据自变量与函数值的对应关系，可得A，B的值，根据顶点式，可得函数解析式；（2）根据函数图像上的点满足函数解析式，可得N点坐标，根据勾股定理，可得答案；（3）根据相似三角形的性质，可得关于m的方程，可得M点的坐标，要分类讨论，以防遗漏．
