题目内容
【题目】如图1,在矩形纸片ABCD中,AB=8,BC=16,将矩形纸片沿EF折叠,使点C与点A重合.
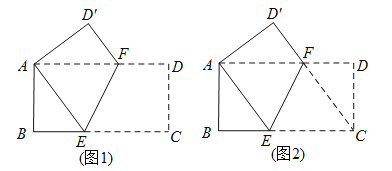
(1)判断△AEF的形状,并说明理由;
(2)求折痕EF的长度;
(3)如图2,展开纸片,连接CF,则点E到CF的距离是 .
【答案】(1)△DEF是等腰三角形,理由见解析;(2)![]() ;(3)8
;(3)8
【解析】
(1)根据折叠和平行的性质,可得∠AEF=∠AFE,即得出结论;
(2)过点E作EM⊥AD于点M,得出四边形ABEM是矩形,设EC=x,则AE=x,BE=16-x,在Rt△ABE中,利用勾股定理求出x,在Rt△EMF中,用勾股定理即可求得;
(3)证明四边形AECF是菱形,设点E到CF的距离为h,通过面积相等,即可求得.
(1)△AEF是等腰三角形.
理由如下:由折叠性质得∠AEF=∠FEC,
在矩形ABCD中,AD∥BC,∴∠AFE=∠FEC,
∴∠AEF=∠AFE, ∴AF=AE;
∴△AEF是等腰三角形;
故答案为:△AEF是等腰三角形.
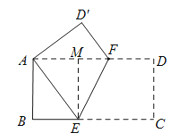
(2)如图,过点E作EM⊥AD于点M,
则∠AME=90°,
又∵在矩形ABCD中,∠BAD=∠B=90°,
∴四边形ABEM是矩形,
∴AM=BE,ME=AB=8,
设EC=x,则AE=x,BE=16-x,
在Rt△ABE中,AE2=AB2+BE2,x2=82+(16-x)2,
解之得x=10,
∴EC=AE=10,BE=6,
∴AM=6,AF=AE=10,
∴MF=AF-AM=4,
在Rt△EMF中,![]() ;
;
故答案为:![]() ;
;
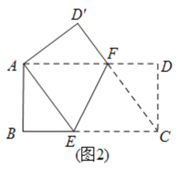
(3)由(1)知,AE=AF=EC,
∵AF∥EC,
∴四边形AECF是平行四边形,
∴四边形AECF是菱形,
设点E到CF的距离为h,
![]() ,
,
∴h=8.即E到CF的距离为8,
故答案为:8.

【题目】已知Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a,b,c,设△ABC的面积为S.
(1)填表:
三边a,b,c | S | c+b-a | c-b+a |
3,4,5 | 6 | ||
5,12,13 | 20 | ||
8,15,17 | 24 |
(2)①如果m=(c+b-a)(c-b+a),观察上表猜想S与m之间的数量关系,并用等式表示出来.
②证明①中的结论.