题目内容
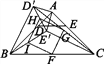
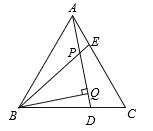
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
【答案】(1)见解析;(2)PE=1.
【解析】
(1)根据等边三角形的性质得到AB=AC,∠BAE=∠C=60°,证明△ABE≌△CAD
(2)根据直角三角形的性质得到BP=2PQ,再根据题意BP=2PQ =4,则PE =1.
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,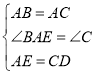 ,
,
∴△ABE≌△CAD(SAS),
(2) ∵△ABE≌△CAD,
∴∠ABE=∠CAQ,
∴∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=∠BAC=60°,∵BQ⊥AD,
∴∠PBQ=90°∠BPQ=90°60°=30°,
∴BP=2PQ.
∵PQ=2,BE=5,
则BP=2PQ =4,PE = BE- PB=5-4=1.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
【题目】近期电影《少年的你》受到广大青少年的喜爱,某校七年级1班2班的几名同学请他们的家长在网上买票,家长了解到某电影院的活动,设购买电影票的张数为![]()
购买张数 |
|
|
|
每张票的价格 |
|
|
|
家长沟通后决定两个班的同学在期中考试结束后去观看。两个班共有![]() 人,期中
人,期中![]() 班人数多于
班人数多于![]() 不足
不足![]() 人。经过估算,如果两个班都以班为单位购买,则一共应付
人。经过估算,如果两个班都以班为单位购买,则一共应付![]() 元。
元。
![]() 求两个班有多少个同学?
求两个班有多少个同学?
![]() 如果两个班联合起来,作为一个团体购票,可以节省多少钱?
如果两个班联合起来,作为一个团体购票,可以节省多少钱?
![]() 如果七年级
如果七年级![]() 班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?