题目内容
【题目】数学活动
问题情境:
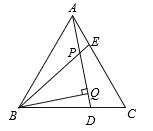
如图1,在ABC中,AB=AC,∠BAC=90°,D,E分别是边AB,AC的中点,将ADE绕点A顺时针旋转α角(0°<α<90°)得到AD′E′,连接CE′,BD′.探究CE′与BD′的数量关系;
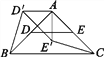 图1
图1 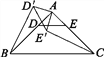 图2
图2 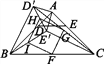 图3
图3 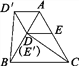 图4
图4
探究发现:
(1)图1中,CE′与BD′的数量关系是________;
(2)如图2,若将问题中的条件“D,E分别是边AB,AC的中点”改为“D为AB边上任意一点,DE∥BC交AC于点E”,其他条件不变,(1)中CE′与BD′的数量关系还成立吗?请说明理由;
拓展延伸:
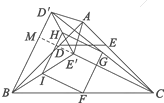
(3)如图3,在(2)的条件下,连接BE′,CD′,分别取BC,CD′,E′D′,BE′的中点F,G,H,I,顺次连接F,G,H,I得到四边形FGHI.请判断四边形FGHI的形状,并说明理由;
(4)如图4,在ABC中,AB=AC,∠BAC=60°,点D,E分别在AB,AC上,且DE∥BC,将ADE绕点A顺时针旋转60°得到AD′E′,连接CE′,BD′.请你仔细观察,提出一个你最关心的数学问题(例如:CE′与BD′相等吗?).
【答案】CE′=BD′
【解析】试题分析:(1)先证明AD=AE,再根据旋转得到∠BAD′=∠CAE′=α,AD′=AE′,证明△ABD′≌△ACE′,根据全等三角形的对应边相等即可得;
(2)类比(1)的方法先证明AD=AE,然后再证明△ABD′≌△ACE′,根据全等三角形的性质即可得;
(3)先证明四边形FGHI是平行四边形,再证明四边形FGHI是菱形, 延长CE交BD′于点M,由(2)得△ABD′≌△ACE′, 从而推导可得∠CBM+∠BCM=90°,进而可推导得到∠IFG=90°,从而得四边形FGHI是正方形;
(4)答案不唯一,只要符合题意即可.
试题解析:(1) ∵D、E分别为AB、AC的中点,∴AD=![]() AB,AE=
AB,AE=![]() AC,
AC,
∵AB=AC,∴AD=AE,
∵△ADE绕点A顺时针旋转α角(0°<α<90°),得到△AD′E′,
∴∠BAD′=∠CAE′=α,AD′=AE′,
在△ABD′和△ACE′中 ,
,
∴△ABD′≌△ACE′,
∴CE′=BD′,
故答案为:CE′=BD′;
(2)CE′与BD′的数量关系还成立,理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB.
∴∠ADE=∠AED,∴ AD=AE,
∵△ADE绕点A顺时针旋转α角(0°<α<90°),得到△AD′E′,
∴∠BAD′=∠CAE′=α,AD′=AE′,
在△ABD′和△ACE′中 ,
,
∴ △ABD′≌△ACE′,
∴ CE′=BD′;
(3)四边形FGHI是正方形,
∵F,G,H,I分别是BC,CD′,E′D′,BE′的中点,
∴FG=HI=![]() BD′,IF=HG=
BD′,IF=HG=![]() CE′.
CE′.
∴四边形FGHI是平行四边形,
又∵BD′=CE′,∴FG=IF,
∴四边形FGHI是菱形,
延长CE交BD‘于点M,如图,
由(2)得△ABD′≌△ACE′,
∴∠ACE′=∠ABD′,
∵∠BAC=90°,
∴∠ACE′+∠ABC+∠BCM=90°,
∴∠ABD′+∠ABC+∠BCM=90°,
∴∠CBM+∠BCM=90°,
又∵FG∥BD′,IF∥CE′,
∴∠CFG=∠CBM,∠BFI=∠BCM,
∴∠CFG+∠BFI=90°,∴∠IFG=90°,
∴四边形FGHI是正方形;
(4)答案不唯一,如:①△ABD′和△ACE′全等吗?
②△BDD′和△CEE′全等吗?
③∠BD′D和∠CE′E相等吗?
④四边形AD′DE是菱形吗?,