题目内容
2013年10月31日20时02分在台湾花莲县,发生6.7级地震,某地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象,已知废墟一侧地面上两探测点A、B 相距3米,探测线与地面夹角分别是30°和 60°(如图),试确定生命所在点 C 的深度。(结果精确到0.1米,参考数据: )
)
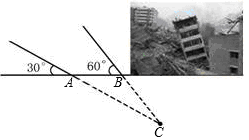
 )
)
2.6.
试题分析:过C作AB的垂线CD,分别用CD表示出AD、BD的值,然后根据AB的长度,列方程求得CD的长,即生命所在点C的深度.
试题解析:如图,过点C作CD⊥AB交AB于点D.
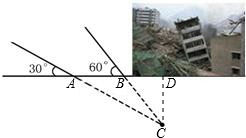
∵探测线与地面的夹角为30°和60°
∴∠CAD=30°,∠CBD=60°
在Rt△BDC中,
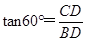
∴
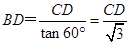
在Rt△ADC中,

∴
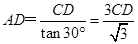
∵AB=AD-BD=3
∴
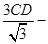

∴
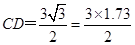 ≈2.6(米).
≈2.6(米). 答:生命所在点C的深度大约为2.6米.
考点: 解直角三角形的应用.

练习册系列答案
相关题目
 中,
中,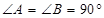 ,
,
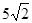 ,点
,点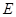 在
在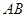 上,
上,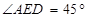 ,
,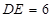 ,
,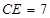 .
.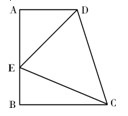
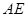 的长;
的长;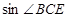 的值.
的值.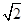 ≈1.414,
≈1.414,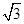 ≈1.732,tan16º≈0.287,sin16º≈0.276,cos16º≈0.961)
≈1.732,tan16º≈0.287,sin16º≈0.276,cos16º≈0.961) 
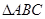 中,
中, ,
,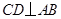 于
于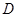 ,
, ,若
,若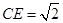 ,
,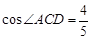 ,求
,求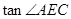 的值及CD的长.
的值及CD的长.
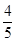 .
.
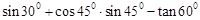 .
.
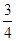
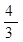
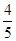
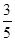
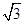 ,则∠A的度数( )
,则∠A的度数( )