题目内容
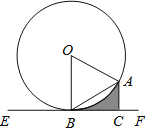
【题目】如图.点![]() 在
在![]() 轴负半轴上,
轴负半轴上,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的点,连接
上的点,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() ,点
,点![]() 在直线
在直线![]() 的上方,则下列结论正确的是( )
的上方,则下列结论正确的是( )

A. ![]() 随
随![]() 的增大而减小B.
的增大而减小B. ![]() 随
随![]() 的增大而增大
的增大而增大
C. ![]() 随
随![]() 的增大而减小D.
的增大而减小D. ![]() 随
随![]() 的增大而增大
的增大而增大
【答案】B
【解析】
先证出△ABC为等边三角形,再求得OA,AB的长,分情况讨论:当点D与点A重合时,点E与点B重合;当点D运动到线段AB中点时,E的坐标变化情况,结合排除法可得解.
∵∠BAC=60°,∠BOA=90°
∴∠ABO=30°
又∵B(0,3![]() ),C(3,0)
),C(3,0)
∴OB=3![]() ,OC=3,从而△ABC为等边三角形
,OC=3,从而△ABC为等边三角形
设OA=x,则AB=2x
∴x2+(3![]() )2=4x2
)2=4x2
解得x=3,即OA=3
∴AB=6
∵以CD为边作等边△CDE
∴当点D与点A重合时,点E与点B重合,此时a=-3,b=0;m=0,n=3![]() 当点D沿着射线AB方向移动时,b变大,显然m也变大,故排除A,但m是否一直变大尚不确定;
当点D沿着射线AB方向移动时,b变大,显然m也变大,故排除A,但m是否一直变大尚不确定;
假设当点D运动到线段AB中点时,由等腰三角形的三线合一性质知CD⊥AB,AD=3,AC=6,
∴CD=3![]() ,∠ACD=30°
,∠ACD=30°
∴∠ACE=90°
∴n=3![]()
此时n的值与点E在点B时的n值相同,故排除C和D
故选:B.

练习册系列答案
相关题目