题目内容
 有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )
有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE(如图),则CD等于( )A.

B.

C.

D.

【答案】分析:首先设CD=xcm,由折叠的性质可得:AD=BD=(8-x)cm,然后在Rt△ACD中,利用勾股定理即可得方程:62+x2=(8-x)2,解此方程即可求得答案.
解答:解:设CD=xcm,则BD=BC-CD=8-x(cm),
由折叠的性质可得:AD=BD=(8-x)cm,
在Rt△ACD中:AC2+CD2=AD2,
即:62+x2=(8-x)2,
解得:x= .
.
∴CD= .
.
故选C.
点评:此题考查了折叠的性质与勾股定理.此题难度不大,注意掌握数形结合思想与方程思想的应用.
解答:解:设CD=xcm,则BD=BC-CD=8-x(cm),
由折叠的性质可得:AD=BD=(8-x)cm,
在Rt△ACD中:AC2+CD2=AD2,
即:62+x2=(8-x)2,
解得:x=
 .
.∴CD=
 .
.故选C.
点评:此题考查了折叠的性质与勾股定理.此题难度不大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
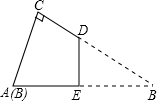 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8cm,D是BC上一点,AD=DB,DE⊥AB,垂足为E,CD等于( )cm.
如图,有一张直角三角形纸片,两直角边AC=6 cm,BC=8cm,D是BC上一点,AD=DB,DE⊥AB,垂足为E,CD等于( )cm.A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,求CD的长.
如图,有一张直角三角形纸片,两直角边AC=6cm,BC=8cm,将△ABC折叠,使点B与点A重合,折痕为DE,求CD的长. 如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为DE,则△ACD的周长为( )
如图,有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与点A重合,折痕为DE,则△ACD的周长为( )