题目内容
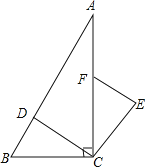
【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=5,CD=4,求BE的长.
【答案】(1)见解析 (2)6
【解析】分析:(1)连接OD,由BD为角平分线得到一对角相等,根据OB=OD,等边对等角得到一对角相等,等量代换得到一对内错角相等,进而确定出OD与BC平行,利用两直线平行同位角相等得到∠ODC为直角,即可得证;
(2)过O作OM垂直于BE,可得出四边形ODCM为矩形,在直角三角形OBM中,利用勾股定理求出BM的长,由垂径定理可得BE=2BM.
详解:(1)连接OD.
∵OD=OB,∴ ∠OBD=∠ODB.
∵BD是∠ABC的角平分线,∴ ∠OBD=∠CBD.
∵ ∠CBD=∠ODB,∴OD∥BC.
∵∠C=90,∴∠ODC=90,∴ OD⊥AC.
∵点D在⊙O上,
∴ AC是⊙O的切线.
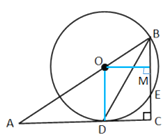
(2)过圆心O作OM![]() BC交BC于M.
BC交BC于M.
∵BE为⊙O 的弦,且OM![]() BE,∴BM=EM,
BE,∴BM=EM,
∵∠ODC=∠C=∠OMC= 90° ,
∴四边形ODCM为矩形,则OM=DC=4.
∵ OB=5,∴BM=![]() =3=EM,
=3=EM,
∴BE=BM+EM=6.

【题目】某快车的计费规则如表1,小明几次乘坐快车的情况如表2,请仔细观察分析表格解答以下问题:
(1)填空:a= ,b= ;
(2)列方程求解表1中的x;
(3)小明的爸爸23:10打快车从机场回家,快车行驶的平均速度是100公里/小时,到家后小明爸爸支付车费603元,请问机场到小明家的路程是多少公里?(用方程解决此问题)
表1:某快车的计费规则
里程费(元/公里) | 时长费(元/分钟) | 远途费(元/公里) | |||
5:00﹣23:00 | a | 9:00﹣18:00 | x | 12公里及以下 | 0 |
23:00﹣次日5:00 | 3.2 | 18:00﹣次日9:00 | 0.5 | 超出12公里的部分 | 1.6 |
(说明:总费用=里程费+时长费+远途费)
表2:小明几次乘坐快车信息
上车时间 | 里程(公里) | 时长(分钟) | 远途费(元) | 总费用(元) |
7:30 | 5 | 5 | 0 | 13.5 |
10:05 | 20 | 18 | 66.7 |