题目内容
【题目】已知，甲、乙两人分别从
两地出发，相向而行，已知甲先出发4分钟后，乙才出发，他们两人在之间的
地相遇，相遇后，甲立即返回
地，乙继续向地前行．甲到达地时停止行走，乙到达地是也停止行走，在整个行走过程中，甲、乙两人均保持各自的速度匀速行走，甲、乙两人相距的路程
（米）与甲出发的时间
（分钟）之间的关系如图所示，则下列结论错误的是（ ）
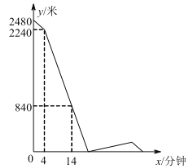
A.两地相距2480米B.甲的速度是60米/分钟，乙的速度是80米/分钟
C.乙出发17分钟后，两人在地相遇D.乙到达地时，甲与地相距的路程是300米．
【答案】C
【解析】
观察函数图像可知A，B两地的路程，可对A作出判断；根据甲先出发4分钟，由图像可得到相应的路程，就可求出甲的速度，再用甲乙的速度和减去甲的速度，可得B的速度，可对B作出判断；根据题意列方程求出相遇的时间，可对C作出判断；求出乙从点C到A所用的时间，然后计算出AC之间的距离，减去甲从相遇后到乙到达
地时走的路程即可对D作出判断．
A、由图可知，
两地相距2480米，A正确；
B、甲的速度是
米/分钟，乙的速度是
米/分钟，B正确；
C、设乙出发x分钟后，两人在
地相遇，
根据题意可得，
，
解得x=16，C错误；
D. 乙到达地所用时间为
分，乙从点C到A所用的时间为31-16=15分，则甲从相遇后行驶的路程为
米，甲与地相距的路程是
米，D正确．
故选C.
金钥匙试卷系列答案【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
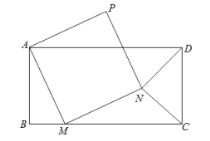
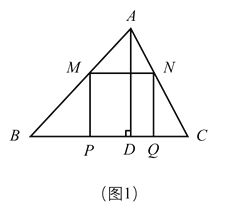
【题目】如图，已知矩形
，点
为线段
上一动点，沿线段由
向
运动，连接
，以为边向右侧作正方形
，连接
，设的路程即
的长为
，
间的距离为
，
间的距离为
．
数学兴趣小组的小刚根据学习函数的经验，分别对函数
随自变量
的变化而变化的规律进行探究，过程如下：
（1）根据下表中自变量的取值进行去电，画图，测量，分别得到几组对应值，请将表格补充完成．
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 2.22 |
| 3 | 4.11 | 5.39 | 6.72 |
| 4.24 | 2.81 | 1.39 | 0 |
| 2.84 | 4.26 |
其中，
，
；
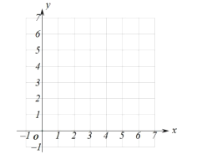
（2）在同一平面黄子佼坐标系中，描点
，并画出的函数图像；
（3）当
为等腰三角形时，的长度约为 ．
