Question

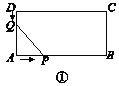
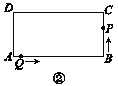
【题目】如图，在平行四边形ABCD中，的平行线交的延长线于点，交的延长线于点，交于点 .

(1)请指出图中平行四边形的个数，并说明理由;

(2)与相等吗?为什么?

Answer 1

【答案】（1）图中平行四边形有3个：平行四边形ABCD、平行四边形AMQC、平行四边形APNC；（2）MP=QN，理由见解析.

【解析】（1）由已知易得图中有3个平行四边形，分别是平行四边形ABCD、平行四边形AMQC和平行四边形APNC，由已知条件根据平行四边形的判定方法进行分析证明即可；

（2）MP=QN，由（1）可知四边形AMQC和四边形APNC都是平行四边形，由此可得MQ=AC=PN，由此可得MQ-PQ=PN-PQ，从而可得MP=QN.

（1）图中平行四边形有3个：平行四边形ABCD、平行四边形AMQC、平行四边形APNC，理由如下：

①四边形ABCD是平行四边形是已知条件；

②四边形APNC是平行四边形的理由：

∵AC∥MN AB∥CD

∴ ∠MPA＝∠PAC ∠MPA＝∠N

∴∠PAC＝∠N

∵AB∥CD

∴ ∠PAC+∠ACN＝180°，∠N+∠APN＝180°，

∴∠ACN＝∠APN，

∴四边形APNC是平行四边形（两组对角分别相等的四边形是平行四边形）

③四边形AMQC是平行四边形的理由：

∵AC∥MN， AD∥BC，

∴ ∠M＝∠DAC ，∠DAC＝∠ACQ，

∴∠M＝∠ACQ，

∵AC∥MN，

∴ ∠M+∠MAC＝180°， ∠MQC+∠ACQ＝180°，

∴∠MAC＝∠MQC，

∴四边形AMQC是平行四边形（两组对角分别相等的四边形是平行四边形）

（2）MP=QN，理由如下：

∵由（1）可知四边形AMQC和四边形APNC都是平行四边形，

∴MQ=AC=PN，

∴MQ-PQ=PN-PQ，

∴MP=QN.