题目内容
【题目】已知:在平面直角坐标系中,边长为8的正方形OABC的两边在坐标轴上(如图).

(1)求点A,B,C的坐标.
(2)经过A,C两点的直线l上有一点P,点D(0,6)在y轴正半轴上,连PD,PB(如图1),若PB2﹣PD2=24,求四边形PBCD的面积.
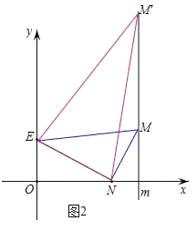
(3)若点E(0,1),点N(2,0)(如图2),经过(2)问中的点P有一条平行于y轴的直线m,在直线m上是否存在一点M,使得△MNE为直角三角形?若存在,求M点的坐标;若不存在,请说明理由.
【答案】(1)A(8,0),B(8,8),C(0,8);(2)15;(3)M的坐标是(3,7)或(3,2)
【解析】
(1)根据正方形的性质直接写出点A,B,C的坐标.
(2)求得直线AC的解析式为y=-x+8,过点P作平行于x轴的直线,根据题意可求点P的坐
标是:P(3,5),故四边形PBCD的面积=S![]() +S
+S![]()
(3)根据第(2)中求得的P(3,5),设M(3,t),分类讨论:
①当∠MEN=90°时,ME![]() =3
=3![]() +(t-1)2,EN
+(t-1)2,EN![]() =1
=1![]() +2
+2![]() ,MN
,MN![]() =1
=1![]() +t
+t![]() ,利用勾股定理求得t的值,
,利用勾股定理求得t的值,
②当∠MNE=90°时,同理可求:M(3,2).
③显然∠EMN不可能等于90°.
综合可得:使△MNE为直角三角形的点是M(3,7)或M(3,2),
(1)∵如图1,四边形OABC是正方形,且其边长为8,
∵.OA=AB=BC=OC=8,
∴A(8,0),B(8,8),C(0,8),
(2)设直线AC的解析式为y=k+8,
将A(8,0)代入,得0=8k+8,
解得k=-1
故直线AC的解析式为y=-x+8.
设P(x,-x+8)
∵PB![]() -PD
-PD![]() =24,D(0,6),B(8,8),
=24,D(0,6),B(8,8),
∴(x-8) ![]() +(-x+8-8)
+(-x+8-8) ![]() -x
-x![]() -(-x+8-6)
-(-x+8-6) ![]() =24,
=24,
解得x=3,
∴点P的坐标是:P(3,5),
∴四边形PBCD的面积=S![]() +S
+S![]() =
=![]() ×2×3+
×2×3+×8×3=15
(3)根据第(2)中求得的P(3,5),设M(3,t),分类讨论:
①当∠MEN=90°时, ME![]() =3
=3![]() +(t-1)
+(t-1) ![]() ,EN
,EN![]() =1
=1![]() +2
+2![]() ,MN
,MN![]() =1
=1![]() +t
+t![]()
∴MN![]() =ME
=ME![]() +EN
+EN![]()
∴1+t![]() =9+t
=9+t![]() -2t+1+5,
-2t+1+5,
∴t=7,
∴M(3,7)
②当∠MNE=90°时,同理可求:M(3,2)
③显然∠EMN不可能等于90°
综合可得:使△MNE为直角三角形的点M的坐标是(3,7)或(3,2).

 智慧小复习系列答案
智慧小复习系列答案