题目内容
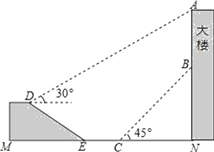
【题目】如图，钟鼓楼AN上悬挂一条幅AB，谢高在坡面D处测得条幅顶部A的仰角为30°，沿坡面向下走到坡脚E处，然后向钟鼓楼方向继续行走10米来到C处，测得条幅的底部B的仰角为45°，此时谢高距钟鼓楼底端N处20米．已知坡面DE=20米，山坡的坡度i=1：
（即tan∠DEM=1：），且M、E、C、N在同一条直线上，求条幅的长度（结果精确到1米）
【答案】17米
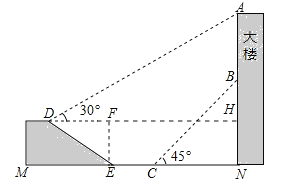
【解析】分析：过点D作DH⊥AN于H，过点E作FE⊥于DH于F，首先求出DF的长，进而可求出DH的长，在直角三角形ADH中，可求出AH的长，进而可求出AN的长，在直角三角形CNB中可求出BN的长，利用AB=AH﹣BN计算即可．
详解：过点D作DH⊥AN于H，过点E作FE⊥于DH于F．
∵坡面DE=20米，山坡的坡度i=1：
，∴EF=10米，DF=10米．
∵DH=DF+EC+CN=（10+30）米，∠ADH=30°，
∴AH=
×DH=（10+10）米，∴AN=AH+EF=（20+10）米．
∵∠BCN=45°，∴CN=BN=20米，∴AB=AN﹣BN=10≈17米．
答：条幅的长度是17米．
练习册系列答案
相关题目
【题目】有20筐橘子，以每筐20千克为标准，超过或不足的部分分别用正数或负数来表示，记录如下：
与标准重量的差(单位：千克) | －2 | －1.5 | －1 | 0 | 1 | 1.5 |
筐 数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)求最重的一筐比最轻的一筐重多少？
(2)求20筐橘子的总重量是多少千克？
【题目】某部队新兵入伍时，对新兵进行“引体向上”测试，以50次为标准，超过50次用正数表示，不足50次用负数表示，第二小队的10名新兵的成绩如下表：
3 |
| 0 | 8 | 7 |
| 10 | 1 |
| 5 |
（1）求第二小队的总成绩；
（2）求第二小队的平均成绩。
