题目内容
【题目】已知：△ABC内接于⊙O，D是弧BC上一点，OD⊥BC，垂足为H．
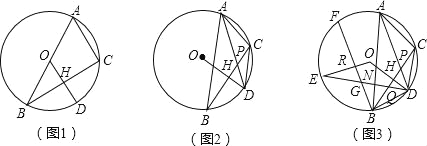
（1）如图1，当圆心O在AB边上时，求证：AC=2OH；
（2）如图2，当圆心O在△ABC外部时，连接AD、CD，AD与BC交于点P，求证：∠ACD=∠APB；
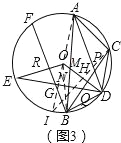
（3）在（2）的条件下，如图3，连接BD，E为⊙O上一点，连接DE交BC于点Q、交AB于点N，连接OE，BF为⊙O的弦，BF⊥OE于点R交DE于点G，若∠ACD﹣∠ABD=2∠BDN，AC=
，BN=
，tan∠ABC=
，求BF的长．
【答案】（1）证明见解析；（2）证明见解析；（3）24.
【解析】
试题分析：（1）易证OH为△ABC的中位线，可得AC=2OH；（2）∠APB=∠PAC+∠ACP，∠ACD=∠ACB+∠BCD，又∵∠PAC =∠BCD，可证∠ACD=∠APB；（3）连接AO延长交于⊙O于点I，连接IC，AB与OD相交于点M，连接OB，易证∠GBN=∠ABC，所以BG=BQ.在Rt△BNQ中，根据tan∠ABC=
，可求得NQ、BQ的长. 利用圆周角定理可求得IC和AI的长度，设QH=x，利用勾股定理可求出QH和HD的长度，利用垂径定理可求得ED的长度，最后利用tan∠OED= 即可求得RG的长度，最后由垂径定理可求得BF的长度．
试题解析：（1）在⊙O中，∵OD⊥BC，∴BH=HC，∵点O是AB的中点，∴AC=2OH；（2）在⊙O中，∵OD⊥BC，∴弧BD=弧CD，∴∠PAC=∠BCD，∵∠APB=∠PAC+∠ACP，∠ACD=∠ACB+∠BCD，∴∠ACD=∠APB；（3）连接AO延长交于⊙O于点I，连接IC，AB与OD相交于点M，连接OB，
∵∠ACD﹣∠ABD=2∠BDN，∴∠ACD﹣∠BDN=∠ABD+∠BDN，∵∠ABD+∠BDN=∠AND，∴∠ACD﹣∠BDN=∠AND，∵∠ACD+∠ABD=180°，∴2∠AND=180°，∴∠AND=90°，∵tan∠ABC=，∴
，∴
，∴
，∵∠BNQ=∠QHD=90°，∴∠ABC=∠QDH，∵OE=OD，
∴∠OED=∠QDH，∵∠ERG=90°，∴∠OED=∠GBN，∴∠GBN=∠ABC，∵AB⊥ED，∴BG=BQ=
，GN=NQ=
，
∵∠ACI=90°，tan∠AIC=tan∠ABC=，∴
，∴IC=
，∴由勾股定理可求得：AI=25，
设QH=x，∵tan∠ABC=tan∠ODE=，∴
，∴HD=2x，∴OH=OD﹣HD=
，BH=BQ+QH=
，
∵OB2=BH2+OH2，∴
，解得：
，当QH=
时，∴QD=
，
∴ND=
，∴MN=
，MD=15,∵
，∴QH=不符合题意，舍去，当QH=
时，∴QD=
∴ND=NQ+QD=
，ED=，∴GD=GN+ND=
,∴EG=ED﹣GD=，∵tan∠OED=
，∴
，
∴EG=
RG，∴RG=
，∴ BR=RG+BG=12,∴BF=2BR=24．
