题目内容
 已知:如图,点D是AB上一点,△ADC与△BDC是等腰三角形且底边分别为AC、BC,求∠ACB的度数.
已知:如图,点D是AB上一点,△ADC与△BDC是等腰三角形且底边分别为AC、BC,求∠ACB的度数.分析:根据三角形内角和定理可得∠A+∠B+∠ACB=180°,再根据等腰三角形的性质可得∠A+∠B=∠ACB,则可求∠ACB的度数.
解答:解:∵△ADC与△BDC是等腰三角形且底边分别为AC、BC,
∴∠A=∠ACD,∠B=∠DCB,
∴∠A+∠B=∠ACB,
∵∠A+∠B+∠ACB=180°,
∴∠ACB=90°.
∴∠A=∠ACD,∠B=∠DCB,
∴∠A+∠B=∠ACB,
∵∠A+∠B+∠ACB=180°,
∴∠ACB=90°.
点评:考查了等腰三角形的性质和三角形内角和定理,得到∠A+∠B=∠ACB是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 BA.
BA.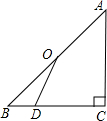 已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点.
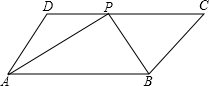
已知:如图,点O是等腰直角△ABC斜边AB的中点,D为BC边上任意一点. 10、已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
10、已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )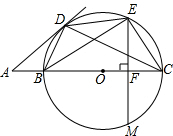 B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2
B=∠DEB,EF⊥BC于点F,交⊙O于点M,EM=2 25、已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥AB,交BC于点G,且DE=DF.
25、已知:如图,点D是△ABC的边AC上的一点,过点D作DE⊥AB,DF⊥BC,E、F为垂足,再过点D作DG∥AB,交BC于点G,且DE=DF.