题目内容
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y= ![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH= ![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2). 
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.
【答案】
(1)
解:由OH=3,tan∠AOH= ![]() ,得
,得
AH=4.即A(﹣4,3).
由勾股定理,得
AO= ![]() =5,
=5,
△AHO的周长=AO+AH+OH=3+4+5=12
(2)
解:将A点坐标代入y= ![]() (k≠0),得
(k≠0),得
k=﹣4×3=﹣12,
反比例函数的解析式为y= ![]() ;
;
当y=﹣2时,﹣2= ![]() ,解得x=6,即B(6,﹣2).
,解得x=6,即B(6,﹣2).
将A、B点坐标代入y=ax+b,得
![]() ,
,
解得 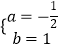 ,
,
一次函数的解析式为y=﹣ ![]() x+1.
x+1.
【解析】(1)根据正切函数,可得AH的长,根据勾股定理,可得AO的长,根据三角形的周长,可得答案;(2)根据待定系数法,可得函数解析式.本题考查了反比例函数与一次函数的交点问题,利用待定系数法是解题关键.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
【题目】某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成就如下表:(单位:分)
项目 | 教学能力 | 科研能力 | 组织能力 |
甲 | 86 | 93 | 73 |
乙 | 81 | 95 | 79 |

(1)根据实际需要,将阅读能力、科研能力、组织能力三项测试得分按5:3:2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.






