题目内容
直线y=kx+b经过点A(0,1),B(-3,0),点P是这条直线上的一个动点,以P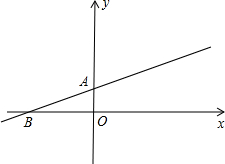 为圆心的圆与x轴相切于点C.
为圆心的圆与x轴相切于点C.
(1)求直线AB的解析式;
(2)设点P的横坐标为t,若⊙P与y轴相切,求t的值;
(3)是否存在点P,使⊙P与y轴两交点间的距离恰好等于2?若存在,求出点P的坐标;若不存在,请说明理由.
 为圆心的圆与x轴相切于点C.
为圆心的圆与x轴相切于点C.(1)求直线AB的解析式;
(2)设点P的横坐标为t,若⊙P与y轴相切,求t的值;
(3)是否存在点P,使⊙P与y轴两交点间的距离恰好等于2?若存在,求出点P的坐标;若不存在,请说明理由.
(1)直线AB的解析式为y=kx+b,
∴
,
∴k=
,b=1,
∴y=
x+1;
(2)设P(t,
t+1),
∵以P为圆心的圆与x轴相切,且⊙P与y轴相切,
∴t=
t+1或-t=
t+1,
∴t=
或t=-
;
(3)假设P点存在,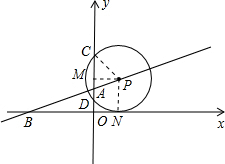
设其坐标为:P(t,
t+1),
过P作PM⊥CD于M,PN⊥x轴于N,连接PC,
则PN=PC=
t+1,PM=t,根据已知CD=2,则CM=1,
∴PC2=PM2+CM2,
∴(
t+1)2=t2+12,
∴t1=0,t2=
,
∴P(0,1)或P(
,
).
∴
|
∴k=
| 1 |
| 3 |
∴y=
| 1 |
| 3 |
(2)设P(t,
| 1 |
| 3 |
∵以P为圆心的圆与x轴相切,且⊙P与y轴相切,
∴t=
| 1 |
| 3 |
| 1 |
| 3 |
∴t=
| 3 |
| 2 |
| 3 |
| 4 |
(3)假设P点存在,

设其坐标为:P(t,
| 1 |
| 3 |
过P作PM⊥CD于M,PN⊥x轴于N,连接PC,
则PN=PC=
| 1 |
| 3 |
∴PC2=PM2+CM2,
∴(
| 1 |
| 3 |
∴t1=0,t2=
| 3 |
| 4 |
∴P(0,1)或P(
| 3 |
| 4 |
| 5 |
| 4 |

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 发以每秒1个单位的速度按照箭头方向通过C、N到M,设P点从O开始运动的路程为x,△AOP的面积为y.
发以每秒1个单位的速度按照箭头方向通过C、N到M,设P点从O开始运动的路程为x,△AOP的面积为y. 置关系时的m的取值范围;
置关系时的m的取值范围; 变化的图象,根据图象解答下列问题:
变化的图象,根据图象解答下列问题: