Question

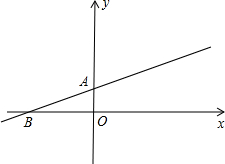
如图，在直角坐标系xoy中，已知两点O₁（3，0）、B（-2，0），⊙O₁与x轴交于原点O和点A，E是y轴上的一个动点，设点E的坐标为（0，m）．
（1）当点O₁到直线BE的距离等于3时，求直线BE的解析式；
（2）当点E在y轴上移动时，直线BE与⊙O₁有哪几种位置关系；直接写出每种位置关系时的m的取值范围；
（3）若在第（1）题中，设∠EBA=α，求sin2α-2sinα•cosα的值．

Answer 1

（1）由已知得BE是⊙O₁的切线，
设切点为M，连接O₁M，则O₁M⊥BM，
∴O₁M=3，BM=4，又OE⊥BO，
∴△BOE∽△BMO，
∴

OE

O1M

=

OB

BM

，
∴

m

3

=

2

4

，
∴m=

3

2

，
设此时直线BE的解析式是y=kx+m，
将B（-2，0）及m=

3

2

代入上式，解得k=

3

4

，
∴y=

3

4

x+

3

2

，
由圆的对称性可得：m=-

3

2

，直线BE也与⊙O₁相切，
同理可得：y₂=-

3

4

x-

3

2

；

（2）当m＞

3

2

或m＜-

3

2

时，直线与圆相离，
当m=

3

2

或m=-

3

2

时，直线与圆相切，
当-

3

2

＜m＜

3

2

时，直线与圆相交；

（3）当直线BE与⊙O₁相切时，显然存在另一条直线BF也与⊙O₁相切，
设直线BE、BF与⊙O₁相切于点M、N，连接O_1M、O₁N，有O_1M⊥BM，O_1N⊥BN，由圆的对称性可知∠EBF=2∠EBO=2∠α，
sinα=

O1M

BO1

=

3

5

，
cosα=

BM

BO1

=

4

5

，
过E作EH⊥BF于H，在△BEF中，
由三角形等积性质得；EH•BF=EF•BO，
BF=BE=

5

2

，EF=2m=3，BO=2，
∴EH=

12

5

，
sin2α=sin∠EBF=

EH

BE

=

12 5

5 2

=

24

25

，
由此可得：sin2α-2sinα•cosα=

24

25

-

3

5

×

4

5

×2=0．