题目内容
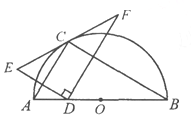
【题目】在圆内接四边形ABCD中,CD为∠BCA外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.
⑴求证△ABD为等腰三角形.
⑵求证ACAF=DFFE
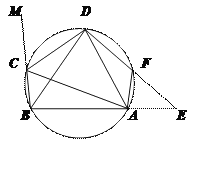
【答案】⑴由圆的性质知∠MCD=∠DAB、∠DCA=∠DBA,而∠MCD=∠DCA,所以∠DBA=∠DAB,故△ABD为等腰三角形.
⑵∵∠DBA=∠DAB
∴弧AD=弧BD
又∵BC=AF
∴弧BC=弧AF、∠CDB=∠FDA
∴弧CD=弧DF
∴CD=DF
再由“圆的内接四边形外角等于它的内对角”知
∠AFE=∠DBA=∠DCA①,∠FAE=∠BDE
∴∠CDA=∠CDB+∠BDA=∠FDA+∠BDA=∠BDE=∠FAE② 由①②得△DCA∽△FAE
∴AC:FE=CD:AF
∴ACAF=" CD" FE
而CD=DF,
∴ACAF=DFFE
【解析】
解决此题关键要用到与圆相关的性质、定理以及三角形相似的判定,等角对等边。
有一定的几何知识的综合性。考查学生审图,分析图中边角关系的解题技能。

练习册系列答案
相关题目