题目内容
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上.将线段AB绕点B顺时针旋转90°,得线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.
(Ⅰ)作出旋转后的图形;
(Ⅱ) ![]() = .
= .

【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)根据图形旋转的性质画出图形即可;
(2)以点B为原点建立坐标系,利用待定系数法求出直线AA′及BC的直线方程,求出D点坐标,利用两点间的距离公式得出BD及CD的长,进而可得出其比值.
试题解析:(1)如图所示;
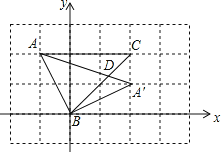
(2)如图,以点B为原点建立坐标系,则A(-1,2),A′(2,1),C(2,2),B(0,0),
设直线AA′的解析式为y=kx+b(k≠0),
则![]() ,
,
解得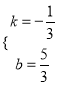 ,
,
故直线AA′的解析式为y=![]() x+
x+![]() ;
;
∵C(2,2),B(0,0),
∴直线BC的解析式为y=x,
∴ ,
,
解得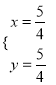 ,
,
∴D(![]() ,
, ![]() ),
),
∴DB=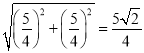 ,CD=
,CD=![]() ,
,
∴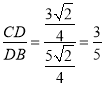 .
.

练习册系列答案
相关题目