题目内容
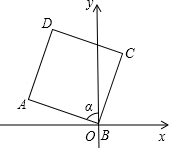 已知边长为1的正方形在坐标系中的位置,如图∠α=75°,求D点的坐标.
已知边长为1的正方形在坐标系中的位置,如图∠α=75°,求D点的坐标.
分析:求D点坐标,需要过D点作y轴的垂线DE,求出线段DE,OE的长,表示D点坐标,根据题目已知及正方形的性质,解直角△OCD,△ODE,用线段的长度表示坐标,注意点D在第二象限的坐标符号.
解答: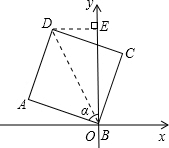 解:作DE⊥y轴于点E,连接BD,
解:作DE⊥y轴于点E,连接BD,
∵∠α=75°,∠COE=90°-75°=15°,∠DOE=∠DOC-∠COE=45°-15°=30°,
在Rt△COD中,OC=CD=1,OD=
,
在Rt△EOD中,∵∠DOE=30°,
∴DE=
OD=
,
OE=
DE=
,
故D(-
,
).
 解:作DE⊥y轴于点E,连接BD,
解:作DE⊥y轴于点E,连接BD,∵∠α=75°,∠COE=90°-75°=15°,∠DOE=∠DOC-∠COE=45°-15°=30°,
在Rt△COD中,OC=CD=1,OD=
| 2 |
在Rt△EOD中,∵∠DOE=30°,
∴DE=
| 1 |
| 2 |
| ||
| 2 |
OE=
| 3 |
| ||
| 2 |
故D(-
| ||
| 2 |
| ||
| 2 |
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,学会角与线段的转化,解直角三角形,用线段的长度表示点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
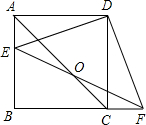 CF.
CF.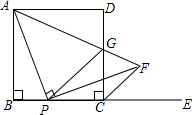 如图,已知边长为2的正方形ABCD,P是BC边上一点,E是BC边延长线上一点,过点P作PF⊥AP与∠DCE的平分线CF交于点F.AF与CD交于点G.
如图,已知边长为2的正方形ABCD,P是BC边上一点,E是BC边延长线上一点,过点P作PF⊥AP与∠DCE的平分线CF交于点F.AF与CD交于点G.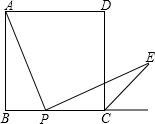 (2013•桂林)如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是( )
(2013•桂林)如图,已知边长为4的正方形ABCD,P是BC边上一动点(与B、C不重合),连结AP,作PE⊥AP交∠BCD的外角平分线于E.设BP=x,△PCE面积为y,则y与x的函数关系式是( )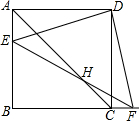 如图,已知边长为4的正方形ABCD,点E在AB上,点F在BC的延长线上,EF与AC交于点H,且AE=CF=m,则四边形EBFD的面积为
如图,已知边长为4的正方形ABCD,点E在AB上,点F在BC的延长线上,EF与AC交于点H,且AE=CF=m,则四边形EBFD的面积为