题目内容
【题目】问题的提出:
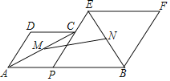
如果点P是锐角△ABC内一动点,如何确定一个位置,使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?
问题的转化:
(1)把ΔAPC绕点A逆时针旋转60度得到![]() 连接
连接![]() 这样就把确定PA+PB+PC的最小值的问题转化成确定
这样就把确定PA+PB+PC的最小值的问题转化成确定![]() 的最小值的问题了,请你利用如图证明:
的最小值的问题了,请你利用如图证明:
![]() ;
;
问题的解决:
(2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时,请你用一定的数量关系刻画此时的点P的位置:_____________________________;
问题的延伸:
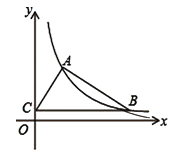
(3)如图是有一个锐角为30°的直角三角形,如果斜边为2,点P是这个三角形内一动点,请你利用以上方法,求点P到这个三角形各顶点的距离之和的最小值.

【答案】(1)证明见解析;(2)∠APB=∠APC=120°;(3)![]() .
.
【解析】
(1)问题的转化:
根据旋转的性质证明△APP'是等边三角形,则PP'=PA,可得结论;
(2)问题的解决:
运用类比的思想,把△APC绕点A逆时针旋转60度得到△AP′C′,连接PP′,由“问题的转化”可知:当B、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,确定当:∠APB=∠APC=120°时,满足三点共线;
(3)问题的延伸:
如图3,作辅助线,构建直角△ABC',利用勾股定理求AC'的长,即是点P到这个三角形各顶点的距离之和的最小值.
问题的转化:
如图1,
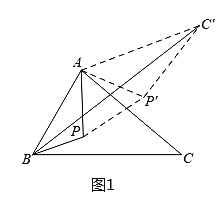
由旋转得:∠PAP'=60°,PA=P'A,
∴△APP'是等边三角形,
∴PP'=PA,
∵PC=P'C,
∴PA+PB+PC=BP+PP′+P′C′.
问题的解决:
满足:∠APB=∠APC=120°时,PA+PB+PC的值为最小;
理由是:如图2,把△APC绕点A逆时针旋转60度得到△AP′C′,连接PP′,
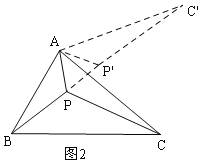
由“问题的转化”可知:当B、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,
∵∠APB=120°,∠APP'=60°,
∴∠APB+∠APP'=180°,
∴B、P、P'在同一直线上,
由旋转得:∠AP'C'=∠APC=120°,
∵∠AP'P=60°,
∴∠AP'C'+∠AP'P=180°,
∴P、P'、C'在同一直线上,
∴B、P、P'、C'在同一直线上,
∴此时PA+PB+PC的值为最小,
故答案为∠APB=∠APC=120°;
问题的延伸:
如图3,
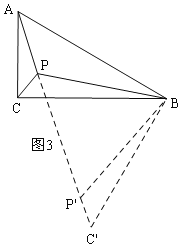
Rt△ACB中,∵AB=2,∠ABC=30°,
∴AC=1,BC=![]() ,
,
把△BPC绕点B逆时针旋转60度得到△BP′C′,连接PP′,
当A、P、P'、C'在同一直线上时,PA+PB+PC的值为最小,
由旋转得:BP=BP',∠PBP'=60°,PC=P'C',BC=BC',
∴△BPP′是等边三角形,
∴PP'=PB,
∵∠ABC=∠APB+∠CBP=∠APB+∠C'BP'=30°,
∴∠ABC'=90°,
由勾股定理得:AC'=![]() ,
,
∴PA+PB+PC=PA+PP'+P'C'=AC'=![]() ,
,
则点P到这个三角形各顶点的距离之和的最小值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案