Question

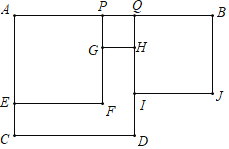
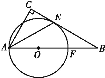
【题目】如图,在Rt△ABC中,∠C=90°,O是AB上一点, ⊙O与BC相切于点E,交AB于点F,连接AE,若AF=2BF,则∠CAE的度数是__.

Answer 1

【答案】30°

【解析】连接OE,EF

利用切线性质得∠OEB=90，再证，AC∥OE.,得∠CAE=∠AEO，根据直角三角形性质，由AF=2BF=2OF,得EF=OF=OE, 得∠OEF=60，所以，∠OEF=60, 所以∠AEO=90-∠OEF=30.

所以，OF=BF,

连接OE,EF

因为，⊙O与BC相切于点E,

所以，∠OEB=90，又∠C=90°，

所以，AC∥OE.,

所以∠CAE=∠AEO，

因为，AF=2BF=2OF,

所以，OF=BF,

所以，EF=OF=OE,

所以，三角形OEF是等边三角形,

所以，∠OEF=60,

所以，∠AEO=90-∠OEF=30

所以，∠CAE=∠AEO=30

故答案为：30