题目内容
【题目】如图,点P是线段AB的中点,Q为线段PB上一点,分别以AQ、AP、PQ、QB为一边作正方形,其面积对应地记作SACDQ,SAEFP,SPGHQ,SQIJB,设AP=m,QB=n,
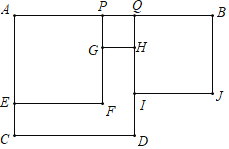
(1)用含有m,n的代数式表示正方形ACDQ的面积SACDQ.
(2)SACDQ+SQIJB与SAEFP+SPGHQ具有怎样的数量关系?并说明理由.
【答案】(1)正方形ACDQ的面积SACDQ=4m2﹣4mn+n2;(2)SACDQ+SQIJB=2(SAEFP+SPGHQ),理由见解析.
【解析】
(1)根据正方形面积公式即可用含有m,n的代数式表示正方形ACDQ的面积SACDQ;
(2)根据正方形的面积即可得SACDQ+SQIJB与SAEFP+SPGHQ的数量关系.
(1)∵点P是线段AB的中点,
∴AP=BP,
分别以AQ、AP、PQ、QB为一边作正方形,
设AP=m,QB=n,
∴PQ=GH=CE=m﹣n,
∴AC=DC=m+m﹣n=2m﹣n,
∴正方形ACDQ的面积SACDQ=(2m﹣n)2=4m2﹣4mn+n2;
(2)SACDQ+SQIJB=2(SAEFP+SPGHQ),理由如下:
∵SACDQ+SQIJB=(2m﹣n)2+n2=4m2﹣4mn+2n2=2(2m2﹣2mn+n2),
SAEFP+SPGHQ=m2+(m﹣n)2=2m2﹣2mn+n2,
∴SACDQ+SQIJB=2(SAEFP+SPGHQ).

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/辆 | -1 | +3 | -2 | +4 | +7 | -5 | -10 |
(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?比原计划是增加(或减少)了多少辆?