题目内容
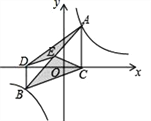
【题目】在平面直角坐标系中,O 为原点,点 A(4,0),点 B(0,3),把△ABO 绕点 B 逆时针旋转,得△A′BO′,点 A、O 旋转后的对应点为 A′、O′,记旋转角为ɑ.
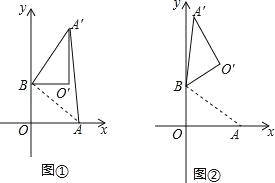
(1)如图 1,若ɑ=90°,求 AA′的长;
(2)如图 2,若ɑ=120°,求点 O′的坐标.
【答案】(1)5![]() ;(2)点O′的坐标为(
;(2)点O′的坐标为(![]() ,
,![]() ).
).
【解析】
(1)由题意可知OA=4,OB=3,由勾股定理求得AB=5.再由旋转的性质可得△ABA′为等腰直角三角形,即可得AA′=![]() BA=5
BA=5![]() ; (2)作O′H⊥y轴于点H,根据旋转的性质可得BO=BO′=3,∠OBO′=120°,即可得∠HBO′=60°.在Rt△BHO′中,∠BO′H′=30°,可得BH=
; (2)作O′H⊥y轴于点H,根据旋转的性质可得BO=BO′=3,∠OBO′=120°,即可得∠HBO′=60°.在Rt△BHO′中,∠BO′H′=30°,可得BH=![]() BO′=
BO′=![]() .再由勾股定理求得O′H=
.再由勾股定理求得O′H=![]() .所以OH=OB+BH=
.所以OH=OB+BH=![]() ,即可得点O′的坐标为(
,即可得点O′的坐标为(![]() ,
,![]() ).
).
(1)∵点A(4,0),点B(0,3),
∴OA=4,OB=3.
∴AB=![]() =5.
=5.
∵△ABO绕点B逆时针旋转90°,得△A′BO′,
∴BA=BA′,∠ABA′=90°.
∴△ABA′为等腰直角三角形,
∴AA′=![]() BA=5
BA=5![]() .
.
(2)作O′H⊥y轴于点H.
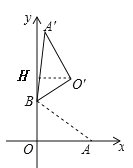
∵△ABO绕点B逆时针旋转120°,得△A′BO′,
∴BO=BO′=3,∠OBO′=120°.
∴∠HBO′=60°.
在Rt△BHO′中,∵∠BO′H=90°-∠HBO′=30°,
∴BH=![]() BO′=
BO′=![]() .
.
∴O′H=![]() .
.
∴OH=OB+BH=3+![]() =
=![]() .
.
∴点O′的坐标为(![]() ,
,![]() ).
).

练习册系列答案
相关题目