Question

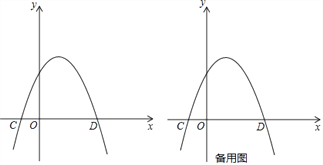
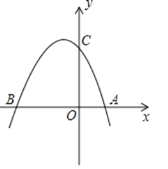
【题目】如图，抛物线y＝﹣x2+mx+2与x轴交于点A，B，与y轴交于点C，点A的坐标为（1，0）

（1）求抛物线的解析式

（2）在抛物线的对称轴l上找一点P，使PA+PC的值最小，求出点P的坐标

（3）在第二象限内的抛物线上，是否存在点M，使△MBC的面积是△ABC面积的？若存在，求出点M的坐标，若不存在，请说明理由．

Answer 1

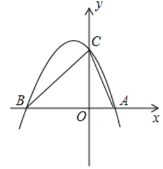
【答案】（1）y＝﹣x2﹣x+2；（2）P（﹣，）；（3）存在，M（﹣1，2）．

【解析】

（1）把点A坐标代入抛物线的解析式求出m即可解决问题；

（2）如图1中，由A、B关于对称轴对称，连接BC交对称轴于P，连接PA，此时PA＋PC的值最小．求出直线BC的解析式，即可解决问题；

（3）存在．如图，连接OM．设M（m，m2m＋2）．由S△MBC＝S△ABC，可得S△OBM＋S△OCMS△ABC＝S△ABC，由此列出方程即可解决问题；

解：（1）∵y＝﹣x2+mx+2经过点A（1，0），

∴0＝﹣1+m+2，

∴m＝﹣1，

∴抛物线的解析式为y＝﹣x2﹣x+2．

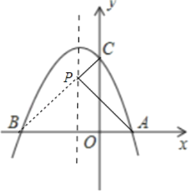
（2）如图，由A、B关于对称轴对称，连接BC交对称轴于P，连接PA，此时PA+PC的值最小．

∵B（﹣2，0），C（0，2），设直线BC的解析式为y＝kx+b，则有，

解得，

∴直线BC的解析式为y＝x+2．

∵抛物线的对称轴x＝﹣，

∴P（﹣，）．

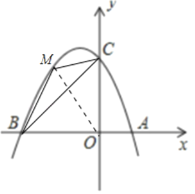
（3）存在．如图，连接OM．设M（m，﹣m2﹣m+2）．

∵S△MBC＝S△ABC，

∴S△OBM+S△OCM﹣S△ABC＝S△ABC，

∴×2×（﹣m2﹣m+2）+×2×（﹣m）＝××2×2，

解得m＝﹣1，

∴M（﹣1，2）．