题目内容
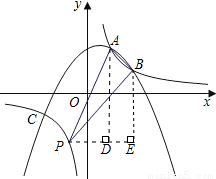
如图,抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和C(-2,-1)三点.(1)求抛物线的解析式;
(2)反比例函数y=
 的图象的一个分支经过点C,并且另个分支与抛物线在第一象限相交.
的图象的一个分支经过点C,并且另个分支与抛物线在第一象限相交.①求出k的值;
②反比函数y=
 的图象是否经过点A和点B,试说明理由;
的图象是否经过点A和点B,试说明理由;③若点P(a,b)是反比例函数y=
 在第三象限的图象上的一个动点,连接AB、PA、PB,请问是否存在这样的一点P使△PAB的面积为3?如果存在,试求出所有符合条件的点P的坐标;如果不存在,请说明理由.
在第三象限的图象上的一个动点,连接AB、PA、PB,请问是否存在这样的一点P使△PAB的面积为3?如果存在,试求出所有符合条件的点P的坐标;如果不存在,请说明理由.
【答案】分析:(1)根据待定系数法将A,B,C三点坐标代入抛物线y=ax2+bx+c中,即可求得抛物线的解析式;
(2)①根据C点的坐标即可求出反比例函数的解析式y=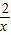 ;②由k的值等于2,若A,B两点的横纵坐标相乘等于2,则反比例函数就经过该点.③直接求△PAB的面积不容易,可以过P作PE∥x轴,作AD⊥PE于D,BE⊥PE于E,先求出四边形ABEP的面积,再减去△BPE的面积,即得△PAB的面积,令其等于3,即可求得满足条件的点P.
;②由k的值等于2,若A,B两点的横纵坐标相乘等于2,则反比例函数就经过该点.③直接求△PAB的面积不容易,可以过P作PE∥x轴,作AD⊥PE于D,BE⊥PE于E,先求出四边形ABEP的面积,再减去△BPE的面积,即得△PAB的面积,令其等于3,即可求得满足条件的点P.
解答:解:(1)∵抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和
C(-2,-1)三点
∴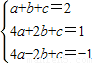
解得: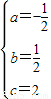 (2分)
(2分)
∴抛物线的解析式为y=- x2+
x2+ +2(3分)
+2(3分)
(2)①反比例函数y=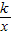 的图象的一个分支经过点C(-2,-1)
的图象的一个分支经过点C(-2,-1)
∴k=(-2)×(-1)=2(5分)
②由①知k的值为2,所以反比例函数的解析式为y=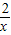 ,
,
∵1×2=2=k,
∴点A(1,2)在反比例函数y=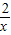 的图象上,
的图象上,
同理点B(2,1)也在反比例函数y=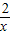 的图象上,
的图象上,
即反比函数y=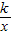 的图象经过点A和点B,(8分)
的图象经过点A和点B,(8分)
③存在(9分)
设点P的坐标为(a,b)
因为点P(a,b)在y=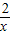 上,
上,
所以点P的坐标为(a,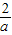 )
)
作PE∥x轴,作AD⊥PE,BE⊥PE,垂足分别为D、E.
则PD=-a+1,PE=-a+2,AD=-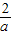 +2,BE=-
+2,BE=-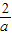 +1(10分)
+1(10分)
∴S△ADP= AD•PD=
AD•PD= (-
(-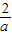 +2)(-a+1)=-a-
+2)(-a+1)=-a-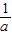 +2
+2
∴S梯形ABED= (AD+BE)•DE=
(AD+BE)•DE= -
-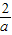
∴S△BPE= PE•BE=-
PE•BE=- a-
a-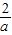 +2
+2
∴S△PAB=S△ADP+S梯形ABED-S△BPE=- a-
a-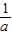 +
+ (12分)
(12分)
若△PAB的面积为3则- a-
a-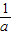 +
+ =3
=3
∴a2+3a+2=0
∴a1=-1,a2=-2
经检验a1=-1,a2=-2都是方程- a-
a-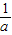 +
+ =3的解
=3的解
所以点P的坐标为(-1,-2)或(-2,-1)(13分)
点评:本题主要考查了待定系数法求反比例函数的解析式,同时在求解三角形的面积时,要灵活的运用割补法进行求解.
(2)①根据C点的坐标即可求出反比例函数的解析式y=
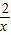 ;②由k的值等于2,若A,B两点的横纵坐标相乘等于2,则反比例函数就经过该点.③直接求△PAB的面积不容易,可以过P作PE∥x轴,作AD⊥PE于D,BE⊥PE于E,先求出四边形ABEP的面积,再减去△BPE的面积,即得△PAB的面积,令其等于3,即可求得满足条件的点P.
;②由k的值等于2,若A,B两点的横纵坐标相乘等于2,则反比例函数就经过该点.③直接求△PAB的面积不容易,可以过P作PE∥x轴,作AD⊥PE于D,BE⊥PE于E,先求出四边形ABEP的面积,再减去△BPE的面积,即得△PAB的面积,令其等于3,即可求得满足条件的点P.解答:解:(1)∵抛物线y=ax2+bx+c经过点A(1,2)、B(2,1)和
C(-2,-1)三点
∴
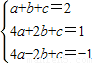

解得:
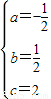 (2分)
(2分)∴抛物线的解析式为y=-
 x2+
x2+ +2(3分)
+2(3分)(2)①反比例函数y=
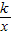 的图象的一个分支经过点C(-2,-1)
的图象的一个分支经过点C(-2,-1)∴k=(-2)×(-1)=2(5分)
②由①知k的值为2,所以反比例函数的解析式为y=
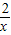 ,
,∵1×2=2=k,
∴点A(1,2)在反比例函数y=
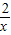 的图象上,
的图象上,同理点B(2,1)也在反比例函数y=
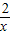 的图象上,
的图象上,即反比函数y=
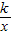 的图象经过点A和点B,(8分)
的图象经过点A和点B,(8分)③存在(9分)
设点P的坐标为(a,b)
因为点P(a,b)在y=
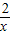 上,
上,所以点P的坐标为(a,
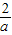 )
)作PE∥x轴,作AD⊥PE,BE⊥PE,垂足分别为D、E.
则PD=-a+1,PE=-a+2,AD=-
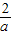 +2,BE=-
+2,BE=-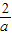 +1(10分)
+1(10分)∴S△ADP=
 AD•PD=
AD•PD= (-
(-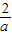 +2)(-a+1)=-a-
+2)(-a+1)=-a-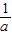 +2
+2∴S梯形ABED=
 (AD+BE)•DE=
(AD+BE)•DE= -
-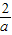
∴S△BPE=
 PE•BE=-
PE•BE=- a-
a-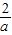 +2
+2∴S△PAB=S△ADP+S梯形ABED-S△BPE=-
 a-
a-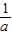 +
+ (12分)
(12分)若△PAB的面积为3则-
 a-
a-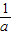 +
+ =3
=3∴a2+3a+2=0
∴a1=-1,a2=-2
经检验a1=-1,a2=-2都是方程-
 a-
a-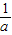 +
+ =3的解
=3的解所以点P的坐标为(-1,-2)或(-2,-1)(13分)
点评:本题主要考查了待定系数法求反比例函数的解析式,同时在求解三角形的面积时,要灵活的运用割补法进行求解.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).