Question

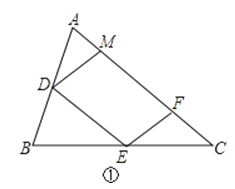
【题目】如图，△ABC的边AB是⊙O的直径，点C在⊙O上，已知AC=6cm，BC=8cm，点P、Q分别在边AB、BC上，且点P不与点A、B重合，BQ=kAP（k＞0），联接PC、PQ．
（1）求⊙O的半径长；
（2）当k=2时，设AP=x，△CPQ的面积为y，求y关于x的函数关系式，并写出定义域；
（3）如果△CPQ与△ABC相似，且∠ACB=∠CPQ，求k的值．

Answer 1

【答案】
（1）解：∵AB是直径，

∴∠ACB=90°，∵AC=6，BC=8，

∴AB= = =10，

∴⊙O的半径为5．

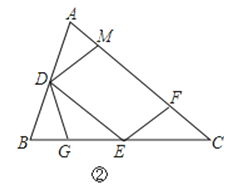
（2）解：如图2中，作PH⊥BC于H．

∵PH∥AC，

∴ = ，

∴ = ，

∴PH= （10﹣x），

∴y= CQPH= （8﹣2x） （10﹣x）= x2﹣ x+24（0＜x＜4）．

（3）解：如图，

∵△CPQ与△ABC相似，∠CPQ=∠ACB=90°，

又∵∠CQP＞∠B，

∴只有∠PCB=∠B，

∴PC=PB，

∵∠B+∠A=90°，∠ACP+∠PCB=90°，

∴∠A=∠ACP，

∴PA=PC=PB=5，

∴△COQ∽△BCA，

∴ = ，

∴ = ，

∴k= ．

【解析】（1）首先证明∠ACB=90°，然后利用勾股定理即可解决问题．（2）如图2中，作PH⊥BC于H．由PH∥AC，推出 = ，推出 = ，推出PH= （10﹣x），根据y= CQPH计算即可．（3）因为△CPQ与△ABC相似，∠CPQ=∠ACB=90°，又因为∠CQP＞∠B，所以只有∠PCB=∠B，推出PC=PB，由∠B+∠A=90°，∠ACP+∠PCB=90°，推出∠A=∠ACP，推出PA=PC=PB=5，由△COQ∽△BCA，推出 = ，推出 = ，即可解决问题．