题目内容
【题目】已知A,B,C,D四点在同一条直线上,点C是线段AB的中点,点D在线段AB上.
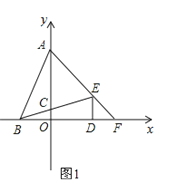
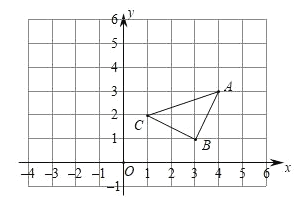
(1)如图1,若AB=12,BD=![]() BC,求线段CD的长度;
BC,求线段CD的长度;
![]()
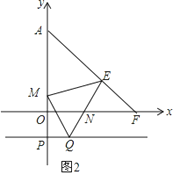
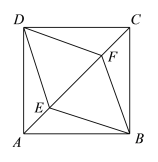
(2)如图2,点E是线段AB上一点,且AE=2BE,当3AD=2BD时,探究线段CD与CE之间的数量关系,请说明理由.
![]()
【答案】(1)4;(2)CD:CE =3:5或5CD=3CE.
【解析】
(1)根据题意,点C是线段AB的中点,则可求得BC的长,由BD=![]() BC,求出BD的长,进而求得CD的长度即可;
BC,求出BD的长,进而求得CD的长度即可;
(2)根据3AD=2BD,设AD=2x,则BD=3x,得AB=5x,AC=![]() AB=
AB=![]() x,由AE=2BE,可得AE=
x,由AE=2BE,可得AE=![]() x,利用线段的差求出CE=AE﹣AC,通过线段的比即可得出线段CD与CE之间的数量关系.
x,利用线段的差求出CE=AE﹣AC,通过线段的比即可得出线段CD与CE之间的数量关系.
解:(1)如图1,∵点C是线段AB的中点,AB=12,
∴BC=![]() AB=6,
AB=6,
∵BD=![]() BC,
BC,
∴BD=2
∴CD=BC﹣BD=6-2=4,
故答案为:4;
![]()
(2)如图2,设AD=2x,则BD=3x,
∴AB=AD+BD=5x,
∵点C是线段AB的中点,
∴AC=![]() AB=
AB=![]() x,
x,
∴CD=AC﹣AD=![]() x,
x,
∵AE=2BE,
∴AE=![]() AB=
AB=![]() x,
x,
CE=AE﹣AC=![]() x,
x,
∴CD:CE=![]() x:
x:![]() x=3:5
x=3:5
或者:5CD=3CE,
故答案为:5CD=3CE.
![]()

【题目】让我们一起来探究“边数大于或等于3的多边形的内角和问题”.
规定:连接多边形不相邻的两个顶点的线段叫做多边形的对角线.
尝试:从多边形某一个顶点出发的对角线可以把一个多边形分成若干个三角形,…….这样,就把“多边形内角和问题”转化为“三角形内角和问题”了.……
(1)请你在下面表格中,试一试,做一做,并将表格补充完整:
名称 | 图形 | 内角和 |
三角形 |
| 180° |
四边形 |
| 2 |
五边形 |
| |
六边形 |
| |
... | ... | …… |
(2)根据上面的表格,请你猜一猜,七边形的内角和等于 ;…….如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和 .
(3)如果一个多边形的内角和是1260°,请判断这个多边形是几边形.