题目内容
【题目】如图,已知点D为OB上的一点,按下列要求进行尺规作图(保留作图痕迹),并回答问题.
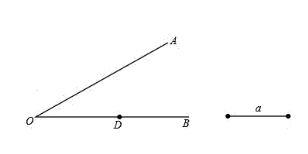
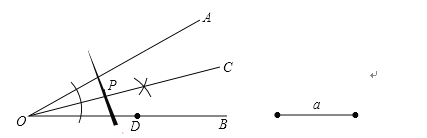
(1)作∠AOB的平分线OC,在OC上取一点P使得OP=a;
(2)过点P作OA边上的高;
(3)在边OA上取一点E,使得PE=PD,请写出∠OEP与∠ODP的数量关系.
【答案】见解析
【解析】
(1)以点O为圆心,以任意长为半径画弧与∠AOB的两边分别相交,再以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,相交于一点,过这一点与O作射线OC即可;在OC上取一点P,使得OP=a;
(2)一点P为原心,任意长半径与OA相交于两点,在以该两点为画弧,两弧交于一点,链接改点与点P,即为所求
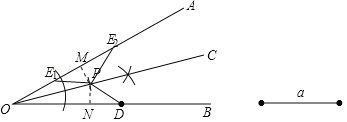
(3)以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,PN⊥OB于N,根据角平分线上的点到角的两边的距离相等可得PM=PN,利用HL证明△E2PM≌△DPN,得出∠OE2P=∠ODP,再根据平角的定义即可求解.
解:(1)如图,OC即为所求;如图,OP=a;
(2) 如图所示.
(3)∠OEP=∠ODP或∠OEP+∠ODP=180°.
理由是:以O为圆心,以OD为半径作弧,交OA于E2,连接PE2,作PM⊥OA于M,
PN⊥OB于N,则PM=PN.
在△E2PM和△DPN中,![]()
∴△E2PM≌△DPN(HL),
∴∠OE2P=∠ODP;
以P为圆心,以PD为半径作弧,交OA于另一点E1,连接PE1,
则此点E1也符合条件PD=PE1,
∵PE2=PE1=PD,
∴∠PE2E1=∠PE1E2,
∵∠OE1P+∠E2E1P=180°,
∵∠OE2P=∠ODP,
∴∠OE1P+∠ODP=180°,
∴∠OEP与∠ODP所有可能的数量关系是:∠OEP=∠ODP或∠OEP+∠ODP=180°.


【题目】抛物线![]() 上部分点坐标如表所示,下列说法错误的是( )
上部分点坐标如表所示,下列说法错误的是( )
x | … | -3 | -2 | -1 | 0 | 1 | … |
y | … | -6 | 0 | 4 | 6 | 6 | … |
A. 抛物线与y轴的交点为(0,6) B. 抛物线的对称轴是在y轴的右侧;
C. 抛物线一定经过点(3,0) D. 在对称轴左侧,y随x增大而减小.