题目内容
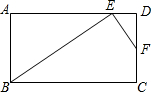
如图,在矩形ABCD中,点M在BC上,DM=DA,AE⊥DM,垂足为E.
求证:(1)DE=MC;(2)AM平分∠BAE.

求证:(1)DE=MC;(2)AM平分∠BAE.

证明:(1)∵ABCD为矩形,
∴∠C=90°,AD∥BC,
∴∠ADE=∠DMC,
又AE⊥DM,得到∠AED=90°,
∴∠C=∠AED=90°,
在△ADE和△DMC中
,
∴△ADE≌△DMC(AAS),
∴DE=MC;
(2)∵ABCD为矩形,
∴AD=BC,∠B=90°,即MB⊥AB,
又AD=DM,
∴BC=DM,
由(1)可知DE=MC,
∴BC-MC=DM-DE,即BM=EM,
又DM⊥AE,MB⊥AB,
∴AM为∠BAE的平分线(在角的内部,到角两边距离相等的点在这个角的平分线上).
∴∠C=90°,AD∥BC,
∴∠ADE=∠DMC,
又AE⊥DM,得到∠AED=90°,
∴∠C=∠AED=90°,
在△ADE和△DMC中
|
∴△ADE≌△DMC(AAS),
∴DE=MC;
(2)∵ABCD为矩形,
∴AD=BC,∠B=90°,即MB⊥AB,
又AD=DM,
∴BC=DM,
由(1)可知DE=MC,
∴BC-MC=DM-DE,即BM=EM,
又DM⊥AE,MB⊥AB,
∴AM为∠BAE的平分线(在角的内部,到角两边距离相等的点在这个角的平分线上).

练习册系列答案
相关题目