题目内容
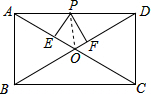
如图所示,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,则PE+PF的值为______.


连接OP,
∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=
S矩形ABCD=
×6×8=12,
在Rt△BAD中,由勾股定理得:BD=
=
=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴
×AO×PE+
×DO×PF=12,
∴5PE+5PF=24,
PE+PF=
,
故答案为:
.
∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=
| 1 |
| 4 |
| 1 |
| 4 |
在Rt△BAD中,由勾股定理得:BD=
| AB2+AD2 |
| 62+82 |
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴5PE+5PF=24,
PE+PF=
| 24 |
| 5 |
故答案为:
| 24 |
| 5 |


练习册系列答案
相关题目




