题目内容
【题目】二次函数y=(m+2)x2﹣2(m+2)x﹣m+5,其中m+2>0.
(1)求该二次函数的对称轴方程;
(2)过动点C(0,n)作直线l⊥y轴.
①当直线l与抛物线只有一个公共点时,求n与m的函数关系;
②若抛物线与x轴有两个交点,将抛物线在x轴下方的部分沿x轴翻折,图象的其余部分保持不变,得到一个新的图象.当n=7时,直线l与新的图象恰好有三个公共点,求此时m的值;
(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求m的取值范围.
【答案】(1)对称轴方程为x=1;(2)①n=﹣2m+3,②m=5;(3)m的取值范围是﹣2<m≤1.
【解析】
(1)将抛物线解析式配方成顶点式即可得;
(2)①画出函数的大致图象,由图象知直线l经过顶点式时,直线l与抛物线只有一个交点,据此可得;
②画出翻折后函数图象,由直线l与新的图象恰好有三个公共点可得-2m+3=-7,解之可得;
(3)由开口向上及函数值都不小于1可得![]() ,解之即可.
,解之即可.
(1)∵y=(m+2)x2﹣2(m+2)x﹣m+5=(m+2)(x﹣1)2﹣2m+3,
∴对称轴方程为x=1.
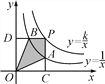
(2)①如图,由题意知直线l的解析式为y=n,

∵直线l与抛物线只有一个公共点,
∴n=﹣2m+3.
②依题可知:当﹣2m+3=﹣7时,直线l与新的图象恰好有三个公共点.
∴m=5.
(3)抛物线y=(m+2)x2﹣2(m+2)x﹣m+5的顶点坐标是(1,﹣2m+3).
依题可得 ![]() ,
,
解得![]() .
.
∴m的取值范围是﹣2<m≤1.

练习册系列答案
相关题目